Jajar Genjang Memiliki Berapa Simetri Lipat? Mari Kita Bedah Tuntas!

Jajar genjang memiliki berapa simetri lipat? Pertanyaan sederhana ini membuka pintu ke dunia geometri yang menakjubkan. Bayangkan sebuah bentuk yang begitu familiar, namun menyimpan rahasia simetri yang menarik. Mari kita selami lebih dalam, mengungkap keindahan yang tersembunyi dalam setiap garis dan sudutnya.

Simetri lipat, konsep yang sering kita temui dalam kehidupan sehari-hari, ternyata memiliki peran penting dalam menentukan karakteristik sebuah bangun datar. Memahami simetri lipat pada jajar genjang tidak hanya bermanfaat dalam pelajaran matematika, tetapi juga membuka mata terhadap keindahan dan keteraturan yang ada di sekitar kita. Bersiaplah untuk menemukan jawaban yang tak hanya memuaskan rasa ingin tahu, tetapi juga menginspirasi.

Memahami Konsep Dasar Simetri Lipat pada Bentuk Geometri: Jajar Genjang Memiliki Berapa Simetri Lipat

Simetri lipat, sebuah konsep fundamental dalam geometri, adalah cermin dari keindahan dan keteraturan yang hadir dalam dunia visual kita. Ia bukan sekadar ide abstrak, melainkan prinsip yang membentuk dasar dari banyak desain dan struktur yang kita lihat sehari-hari. Memahami simetri lipat membuka mata kita terhadap harmoni yang tersembunyi dalam bentuk, membantu kita menghargai estetika yang dibangun berdasarkan keseimbangan dan proporsi.

Lebih dari itu, simetri lipat adalah kunci untuk memahami sifat-sifat geometris yang mendasar, memungkinkan kita untuk memprediksi dan menganalisis perilaku bentuk dalam berbagai konteks.

Simetri lipat, juga dikenal sebagai simetri bilateral, terjadi ketika sebuah bentuk dapat dibagi menjadi dua bagian yang identik melalui sebuah garis atau sumbu. Jika kita melipat bentuk tersebut sepanjang garis simetri, kedua bagian akan saling menutupi dengan sempurna. Garis simetri ini, yang sering disebut sebagai garis lipat atau sumbu simetri, adalah kunci untuk memahami konsep ini. Konsep ini berlaku luas, mulai dari bentuk sederhana seperti lingkaran dan persegi, hingga bentuk yang lebih kompleks seperti bintang dan bahkan struktur tiga dimensi.

Pada dasarnya, simetri lipat adalah tentang keseimbangan dan refleksi. Setiap titik pada satu sisi garis simetri memiliki korespondensi yang identik pada sisi lainnya. Pemahaman yang mendalam tentang simetri lipat tidak hanya penting dalam matematika, tetapi juga dalam seni, desain, dan bahkan dalam ilmu pengetahuan alam, di mana banyak organisme dan struktur mengikuti prinsip simetri.

Definisi Simetri Lipat dan Penerapannya pada Berbagai Bentuk Geometris

Simetri lipat adalah sifat suatu bentuk geometri yang memungkinkan bentuk tersebut dibagi menjadi dua bagian yang identik melalui sebuah garis atau sumbu. Bayangkan sebuah cermin yang ditempatkan di sepanjang garis ini; kedua sisi bentuk akan menjadi bayangan cermin satu sama lain. Ini berarti setiap titik pada satu sisi garis simetri memiliki padanan yang sama persis pada sisi lainnya. Konsep ini melampaui bentuk-bentuk sederhana dan dapat diterapkan pada berbagai objek, dari bentuk dua dimensi hingga objek tiga dimensi yang lebih kompleks.

Mari kita mulai dengan hal-hal yang membuat kita takjub: contoh listrik statis , yang seringkali tampak seperti sihir! Lalu, pikirkan tentang betapa istimewanya kita, karena secara geografis indonesia terletak diantara dua benua yaitu , posisi yang membuat kita kaya akan keberagaman. Selanjutnya, pelajari bagaimana ciri perkembangbiakan hewan secara vegetatif adalah cara alam menunjukkan keajaiban.

Terakhir, jangan lupakan kekuatan seni: fungsi pola lantai dalam tarian adalah kunci untuk menciptakan keindahan yang tak terlupakan.

Dalam konteks bentuk dua dimensi, garis simetri adalah garis lipat yang memungkinkan bentuk dilipat sehingga kedua bagiannya saling menutupi. Jumlah garis simetri yang dimiliki oleh suatu bentuk bervariasi tergantung pada bentuknya. Beberapa bentuk mungkin memiliki satu garis simetri, sementara yang lain mungkin memiliki lebih dari satu, bahkan tak terhingga banyaknya.

Sebagai contoh, sebuah lingkaran memiliki simetri lipat tak terbatas karena setiap garis yang melewati pusat lingkaran adalah garis simetri. Persegi memiliki empat garis simetri, dua yang melewati sisi-sisi yang berlawanan dan dua yang melewati diagonal. Segitiga sama sisi memiliki tiga garis simetri, masing-masing melewati satu sudut dan titik tengah sisi yang berlawanan. Sementara itu, jajar genjang, kecuali jika ia juga merupakan persegi panjang, hanya memiliki simetri putar tetapi tidak memiliki simetri lipat.

Pemahaman tentang simetri lipat membantu kita mengklasifikasikan bentuk berdasarkan sifat-sifat geometrisnya, dan juga membantu kita dalam memecahkan masalah yang berkaitan dengan luas, keliling, dan volume. Konsep ini sangat penting dalam bidang desain, arsitektur, dan seni, di mana keseimbangan dan proporsi adalah kunci untuk menciptakan karya yang estetis dan harmonis.

Simetri lipat juga penting dalam studi struktur molekul dalam kimia, serta dalam analisis pola dalam alam, seperti pola pada daun atau bentuk kristal. Pemahaman yang kuat tentang simetri lipat memungkinkan kita untuk mengidentifikasi pola, memprediksi sifat-sifat, dan menciptakan desain yang efektif dan estetis. Dengan kata lain, simetri lipat adalah alat yang ampuh untuk memahami dan mengapresiasi dunia di sekitar kita, yang memberikan dasar untuk pemahaman yang lebih dalam tentang matematika dan ilmu pengetahuan.

Perbandingan Jumlah Simetri Lipat pada Beberapa Bentuk Dasar

Jumlah simetri lipat yang dimiliki oleh suatu bentuk adalah karakteristik penting yang membedakan bentuk tersebut dari bentuk lainnya. Tabel di bawah ini memberikan gambaran tentang jumlah simetri lipat pada beberapa bentuk dasar geometri, membantu kita untuk lebih memahami perbedaan dan persamaan di antara mereka.

Mari kita mulai dengan hal yang seru: pernahkah kamu merasakan rambut berdiri saat menyisir? Itu adalah contoh listrik statis , fenomena alam yang ajaib! Selanjutnya, bayangkan betapa strategisnya posisi negara kita, karena secara geografis indonesia terletak diantara dua benua yaitu Asia dan Australia, memberikan kita kekayaan budaya dan sumber daya yang luar biasa. Kemudian, bicara soal kehidupan, ciri perkembangbiakan hewan secara vegetatif adalah cara alam menciptakan keajaiban tanpa batas.

Akhirnya, jangan lupakan seni, karena fungsi pola lantai dalam tarian adalah kunci untuk menyampaikan cerita dan emosi, sebuah bentuk ekspresi yang memukau. Ayo terus belajar dan berkembang!

Bentuk Geometri	Jumlah Simetri Lipat	Deskripsi Garis Simetri	Contoh
Persegi	4	Dua garis yang menghubungkan titik tengah sisi yang berlawanan, dan dua garis diagonal.	Jendela, ubin lantai
Persegi Panjang	2	Garis yang menghubungkan titik tengah sisi yang berlawanan.	Pintu, kartu nama
Lingkaran	Tak Terhingga	Setiap garis yang melewati pusat lingkaran.	Roda, jam dinding
Segitiga Sama Sisi	3	Garis yang menghubungkan satu sudut ke titik tengah sisi yang berlawanan.	Tanda peringatan, atap rumah

Contoh Nyata Simetri Lipat dalam Kehidupan Sehari-hari

Simetri lipat hadir di mana-mana, sering kali tanpa kita sadari. Penerapannya sangat luas, dari desain logo yang ikonik hingga arsitektur bangunan yang megah. Pemahaman tentang simetri lipat tidak hanya memperkaya apresiasi estetika kita, tetapi juga memberikan wawasan tentang prinsip-prinsip desain yang efektif.

• Desain Logo: Banyak logo perusahaan dan merek terkenal menggunakan simetri lipat untuk menciptakan kesan keseimbangan, stabilitas, dan profesionalisme. Contohnya adalah logo Toyota, yang menggunakan simetri lipat untuk menciptakan tampilan yang harmonis dan mudah diingat.
• Arsitektur: Simetri lipat sering digunakan dalam desain bangunan untuk menciptakan struktur yang menarik secara visual dan stabil secara struktural. Katedral, kuil, dan bangunan pemerintahan sering kali dirancang dengan simetri lipat untuk menciptakan rasa keagungan dan keteraturan.
• Seni: Dalam seni, simetri lipat digunakan untuk menciptakan komposisi yang seimbang dan menarik. Seniman sering menggunakan simetri lipat untuk menciptakan karya yang estetis dan mudah dinikmati.
• Alam: Simetri lipat juga ditemukan dalam alam, misalnya pada pola pada sayap kupu-kupu, bentuk bunga, dan bahkan wajah manusia. Ini menunjukkan bahwa simetri adalah prinsip dasar yang mengatur banyak aspek dunia di sekitar kita.

Demonstrasi Melipat Jajar Genjang untuk Menemukan Garis Simetri Lipat

Meskipun jajar genjang pada umumnya tidak memiliki simetri lipat (kecuali jika ia adalah persegi panjang atau belah ketupat), kita dapat melakukan percobaan untuk lebih memahami konsep ini. Berikut adalah langkah-langkah untuk mencoba menemukan garis simetri lipat pada jajar genjang:

1. Siapkan Jajar Genjang: Ambil selembar kertas berbentuk jajar genjang. Pastikan semua sisinya tidak sama panjang.
2. Lipat Uji Coba: Coba lipat kertas tersebut menjadi dua bagian yang sama. Perhatikan apakah kedua sisi saling menutupi dengan sempurna. Jika tidak, berarti jajar genjang tersebut tidak memiliki simetri lipat.
3. Analisis: Perhatikan bahwa pada jajar genjang, tidak ada garis yang dapat membagi bentuk menjadi dua bagian yang identik, kecuali jika jajar genjang tersebut adalah persegi panjang (dengan dua garis simetri) atau belah ketupat (dengan dua garis simetri).

Melalui percobaan ini, kita dapat mengamati langsung bagaimana bentuk-bentuk geometri tertentu tidak memenuhi kriteria simetri lipat. Hal ini memperkuat pemahaman kita tentang konsep tersebut dan membantu kita membedakan antara bentuk yang simetris dan yang tidak.

“Simetri, sejauh yang kita pahami, adalah ide yang mendasar yang mengikat alam semesta bersama-sama.”

Hermann Weyl

Eksplorasi Sifat-Sifat Jajar Genjang yang Berhubungan dengan Simetri Lipat

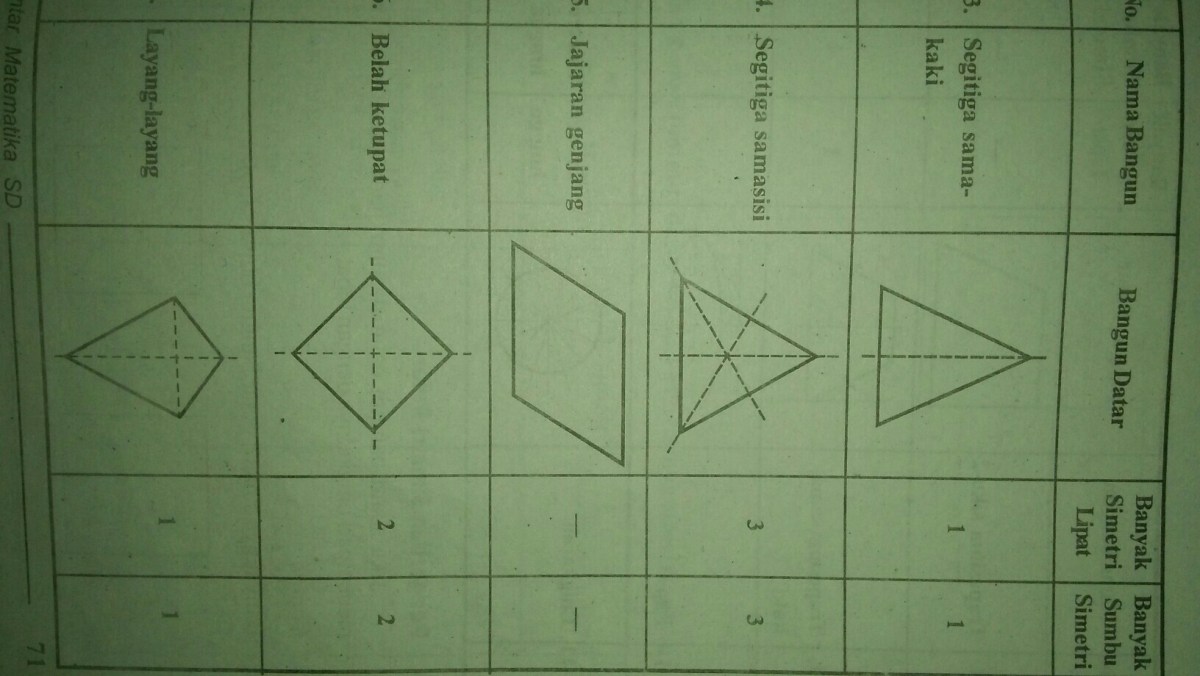
Jajar genjang, bangun datar yang sering kita temui, menyimpan keunikan dalam simetri lipatnya. Memahami bagaimana sifat-sifat jajar genjang memengaruhi simetri lipatnya akan membuka wawasan baru tentang dunia geometri. Mari kita selami lebih dalam untuk mengungkap rahasia di balik simetri lipat pada jajar genjang.

Simetri lipat, juga dikenal sebagai simetri bilateral, adalah ketika sebuah bangun datar dapat dilipat menjadi dua bagian yang sama persis. Garis lipatan ini disebut sebagai garis simetri. Jumlah garis simetri yang dimiliki suatu bangun datar sangat bergantung pada bentuk dan sifat-sifatnya. Dalam konteks jajar genjang, jumlah garis simetri bisa bervariasi, bahkan bisa tidak memiliki sama sekali, tergantung pada jenis dan proporsi bangun tersebut.

Mari kita telusuri lebih lanjut.

Sifat-Sifat Jajar Genjang yang Memengaruhi Simetri Lipat

Sifat-sifat jajar genjang, seperti kesamaan sisi, sudut, dan diagonal, sangat menentukan jumlah simetri lipat yang dimilikinya. Mari kita bedah lebih detail:

• Kesamaan Sisi: Pada jajar genjang umum, sisi-sisi yang berhadapan sama panjang. Namun, sisi-sisi yang berdekatan umumnya tidak sama panjang. Hal ini memengaruhi simetri lipat. Jajar genjang umum hanya memiliki simetri lipat jika memenuhi kriteria khusus (misalnya, menjadi persegi panjang atau belah ketupat).
• Besar Sudut: Sudut-sudut yang berhadapan pada jajar genjang selalu sama besar, sedangkan sudut-sudut yang berdekatan saling berpelurus (jumlahnya 180 derajat). Perbedaan besar sudut ini juga berperan penting dalam menentukan ada tidaknya simetri lipat.
• Diagonal: Diagonal jajar genjang membagi jajar genjang menjadi dua segitiga yang kongruen. Diagonal juga berpotongan di titik tengah masing-masing. Pada jajar genjang umum, diagonal tidak saling tegak lurus dan tidak membagi sudut-sudut pada titik potongnya menjadi dua sama besar. Namun, pada jajar genjang khusus (seperti persegi panjang dan belah ketupat), diagonal memiliki sifat-sifat yang lebih istimewa yang memengaruhi simetri lipat.

Perhatikan bagaimana sifat-sifat ini berinteraksi. Jika sebuah jajar genjang memiliki semua sisi sama panjang dan sudut-sudutnya siku-siku (90 derajat), maka ia berubah menjadi persegi. Persegi memiliki empat simetri lipat. Sebaliknya, jika jajar genjang memiliki sisi-sisi yang tidak sama panjang dan sudut-sudut yang tidak siku-siku, maka ia tidak memiliki simetri lipat sama sekali.

Perbedaan Simetri Lipat pada Jajar Genjang Umum dan Khusus

Jajar genjang dapat diklasifikasikan menjadi dua kategori utama: jajar genjang umum dan jajar genjang khusus. Perbedaan utama terletak pada sifat-sifat sisi, sudut, dan diagonalnya, yang secara langsung memengaruhi jumlah simetri lipatnya:

• Jajar Genjang Umum: Jajar genjang umum hanya memiliki sisi-sisi yang berhadapan sama panjang dan sudut-sudut yang berhadapan sama besar. Bentuk ini umumnya tidak memiliki simetri lipat. Garis simetri hanya ada jika jajar genjang tersebut memiliki karakteristik tambahan yang membuatnya memenuhi syarat sebagai persegi panjang atau belah ketupat.
• Persegi Panjang: Persegi panjang adalah jajar genjang khusus dengan semua sudut siku-siku. Ia memiliki dua simetri lipat: satu melalui garis yang menghubungkan titik tengah sisi-sisi yang berlawanan, dan satu lagi melalui garis yang sama, tetapi tegak lurus terhadap garis pertama.
• Belah Ketupat: Belah ketupat adalah jajar genjang khusus dengan semua sisi sama panjang. Ia juga memiliki dua simetri lipat, yang bertepatan dengan diagonal-diagonalnya.
• Persegi: Persegi adalah jajar genjang khusus yang merupakan kombinasi dari persegi panjang dan belah ketupat. Ia memiliki empat simetri lipat: dua melalui garis yang menghubungkan titik tengah sisi-sisi yang berlawanan, dan dua lagi melalui diagonal-diagonalnya.

Perbedaan ini menunjukkan bahwa semakin simetris sifat-sifat jajar genjang (misalnya, semua sisi sama panjang atau semua sudut siku-siku), semakin banyak simetri lipat yang dimilikinya.

Pengaruh Perubahan Ukuran Sudut dan Panjang Sisi pada Simetri Lipat

Perubahan pada ukuran sudut atau panjang sisi jajar genjang secara signifikan memengaruhi simetri lipatnya. Mari kita lihat bagaimana hal ini terjadi:

• Perubahan Ukuran Sudut: Jika kita mulai dengan persegi panjang (dua simetri lipat) dan secara bertahap mengubah sudut-sudutnya, kita akan mendapatkan jajar genjang umum. Saat sudut-sudutnya tidak lagi siku-siku, simetri lipatnya hilang. Perubahan sudut menggeser bentuk, merusak kesimetrisan yang ada.
• Perubahan Panjang Sisi: Jika kita mulai dengan belah ketupat (dua simetri lipat) dan mengubah panjang sisi-sisinya sedemikian rupa sehingga sisi-sisi yang berdekatan tidak lagi sama panjang, kita akan mendapatkan jajar genjang umum. Dalam kasus ini, simetri lipatnya juga hilang. Perubahan panjang sisi mengubah proporsi bentuk, menghilangkan kesimetrisan.

Contohnya, bayangkan sebuah persegi. Jika kita “mendorong” salah satu sudutnya sehingga menjadi tidak siku-siku, kita akan mendapatkan jajar genjang. Simetri lipat yang awalnya ada pada persegi (empat garis simetri) kini hilang, menyisakan hanya dua garis simetri jika kita tetap mempertahankan bentuk persegi panjang. Perubahan kecil pada sudut atau panjang sisi dapat mengubah secara dramatis sifat simetri lipatnya.

Contoh Soal Matematika

Mari kita lihat beberapa contoh soal matematika yang melibatkan perhitungan simetri lipat pada jajar genjang:

• Soal 1: Sebuah jajar genjang memiliki panjang sisi 10 cm dan 15 cm. Sudut-sudutnya tidak ada yang siku-siku. Berapa banyak simetri lipat yang dimiliki jajar genjang ini? (Jawaban: 0)
• Soal 2: Sebuah persegi panjang memiliki panjang 8 cm dan lebar 6 cm. Berapa banyak simetri lipat yang dimiliki persegi panjang ini? (Jawaban: 2)
• Soal 3: Sebuah belah ketupat memiliki panjang diagonal 12 cm dan 16 cm. Berapa banyak simetri lipat yang dimiliki belah ketupat ini? (Jawaban: 2)
• Soal 4: Sebuah persegi memiliki sisi 7 cm. Berapa banyak simetri lipat yang dimiliki persegi ini? (Jawaban: 4)

Soal-soal ini menekankan pentingnya memahami sifat-sifat jajar genjang untuk menentukan jumlah simetri lipatnya. Ingatlah bahwa jajar genjang umum (dengan sisi dan sudut yang tidak istimewa) cenderung tidak memiliki simetri lipat, sementara jajar genjang khusus (seperti persegi panjang, belah ketupat, dan persegi) memiliki simetri lipat berdasarkan sifat-sifat khususnya.

Poin-Poin Penting tentang Sifat-Sifat Jajar Genjang dan Simetri Lipat

Untuk memudahkan pemahaman dan mengingat konsep simetri lipat pada jajar genjang, berikut adalah daftar poin-poin penting yang perlu diingat:

• Jajar genjang umum (sisi berhadapan sama panjang, sudut berhadapan sama besar) umumnya tidak memiliki simetri lipat.
• Persegi panjang memiliki dua simetri lipat.
• Belah ketupat memiliki dua simetri lipat.
• Persegi memiliki empat simetri lipat.
• Simetri lipat sangat dipengaruhi oleh kesamaan sisi, besar sudut, dan sifat diagonal.
• Perubahan pada ukuran sudut atau panjang sisi dapat mengubah jumlah simetri lipat.

Dengan memahami poin-poin ini, kita dapat lebih mudah mengidentifikasi dan menghitung simetri lipat pada berbagai jenis jajar genjang.

Mengungkap Jumlah Simetri Lipat yang Dimiliki Jajar Genjang

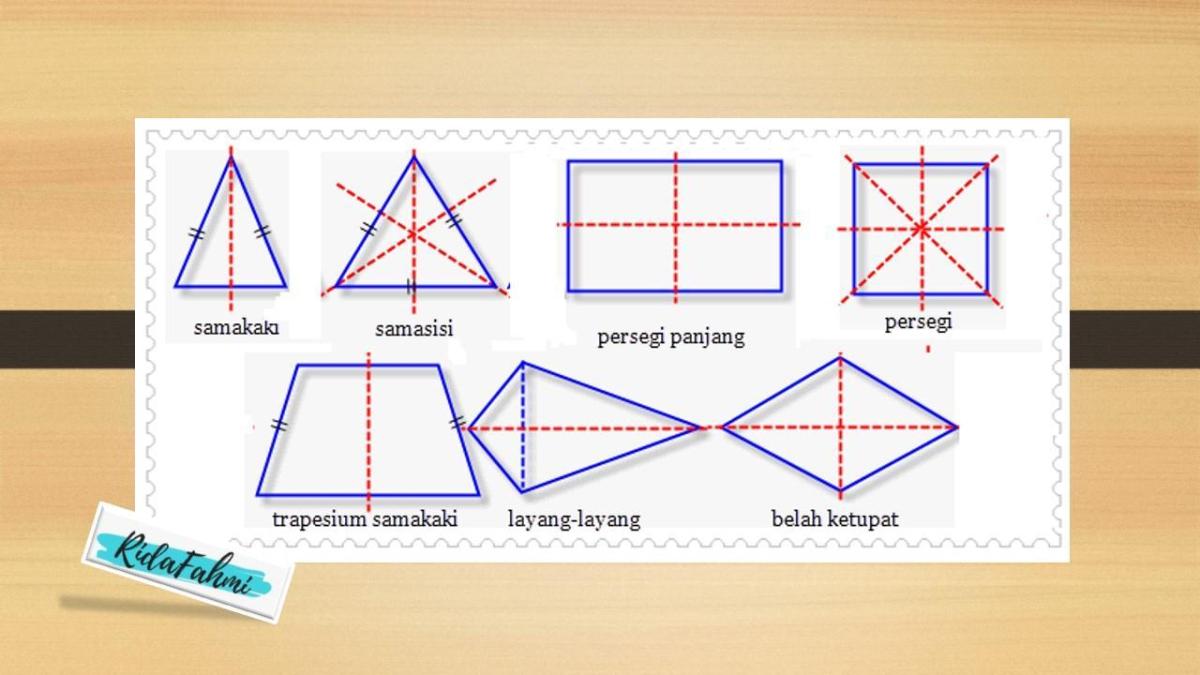
Jajar genjang, dengan keanggunan garis sejajarnya, seringkali menjadi objek kajian menarik dalam dunia geometri. Namun, pertanyaan tentang simetri lipatnya kerap kali mengundang perdebatan. Mari kita selami lebih dalam untuk mengungkap kebenaran di balik simetri lipat pada bangun datar yang satu ini.

Jumlah Simetri Lipat Jajar Genjang: Kasus Umum dan Khusus

Jajar genjang pada umumnya, memiliki karakter unik yang membedakannya dari bentuk-bentuk geometri lainnya. Mari kita bedah secara mendalam mengenai jumlah simetri lipat yang dimilikinya, dengan mengacu pada prinsip-prinsip matematika yang kokoh.

Pada jajar genjang secara umum, hanya terdapat satu titik pusat simetri, yaitu titik potong kedua diagonalnya. Namun, ia tidak memiliki garis simetri lipat. Garis simetri lipat adalah garis yang membagi bangun menjadi dua bagian yang identik saat dilipat. Pada jajar genjang, tidak ada garis seperti itu yang dapat membagi bangun menjadi dua bagian yang saling menutupi dengan sempurna. Jika kita mencoba melipat jajar genjang sepanjang diagonalnya, kedua bagian tidak akan saling menutupi dengan tepat, kecuali jika jajar genjang tersebut merupakan bentuk khusus seperti persegi panjang atau belah ketupat.

Secara matematis, simetri lipat berkaitan erat dengan kemampuan suatu bangun untuk dipetakan pada dirinya sendiri melalui lipatan. Jajar genjang tidak memenuhi kriteria ini. Jika kita mengambil sembarang garis yang melewati pusat simetri, dan mencoba melipat jajar genjang sepanjang garis tersebut, kita akan melihat bahwa kedua bagian tidak akan saling berimpit. Hal ini disebabkan oleh sifat dasar jajar genjang yang memiliki sisi-sisi berhadapan yang sama panjang dan sejajar, namun sudut-sudutnya tidak selalu sama besar.

Kondisi ini menghalangi adanya garis simetri lipat.

Mari kita bandingkan dengan bentuk-bentuk khusus. Persegi panjang, yang merupakan jajar genjang dengan sudut siku-siku, memiliki dua simetri lipat, yaitu garis yang melewati tengah sisi-sisi yang berhadapan. Belah ketupat, yang merupakan jajar genjang dengan semua sisi sama panjang, juga memiliki dua simetri lipat, yaitu garis yang melewati diagonal-diagonalnya. Perbedaan ini menunjukkan bahwa jumlah simetri lipat sangat bergantung pada sifat-sifat khusus suatu bangun.

Ilustrasi Garis Simetri Lipat pada Jajar Genjang

Meskipun jajar genjang umum tidak memiliki simetri lipat, mari kita bayangkan bagaimana garis simetri akan terlihat jika ada. Kita bisa membayangkan dua garis yang akan membagi jajar genjang menjadi dua bagian yang identik. Namun, karena tidak ada garis semacam itu, kita hanya bisa membayangkan posisi garis tersebut jika jajar genjang adalah bentuk khusus. Pada persegi panjang, garis simetri akan membagi bangun menjadi dua bagian yang sama persis, sejajar dengan sisi-sisinya.

Pada belah ketupat, garis simetri akan melewati diagonal-diagonalnya.

Jika kita menggambar jajar genjang, kita bisa membayangkan garis yang melewati titik tengah sisi atas dan bawah, serta garis yang melewati titik tengah sisi kiri dan kanan. Namun, jika kita melipat jajar genjang sepanjang garis-garis ini, kedua bagian tidak akan saling menutupi. Hal ini menjadi bukti bahwa jajar genjang umum tidak memiliki simetri lipat.

Simulasi Sederhana Simetri Lipat Jajar Genjang

Bayangkan kita memiliki jajar genjang yang terbuat dari kertas. Kita bisa memutarnya di sekitar titik pusat simetrinya, yaitu titik potong kedua diagonal. Saat kita memutar jajar genjang 180 derajat, bangun tersebut akan kembali ke posisi semula. Namun, selama proses pemutaran, tidak ada posisi di mana bangun tersebut terlihat identik dengan dirinya sendiri melalui lipatan. Hal ini menunjukkan bahwa tidak ada garis simetri lipat yang dapat ditemukan.

Kita juga bisa mencoba melipat jajar genjang sepanjang diagonal-diagonalnya. Namun, kedua bagian tidak akan saling menutupi dengan sempurna. Jika kita mencoba melipat sepanjang garis yang menghubungkan titik tengah sisi-sisi yang berhadapan, hal yang sama juga akan terjadi. Simulasi sederhana ini membantu kita memahami konsep bahwa jajar genjang umum tidak memiliki simetri lipat.

Tips Memahami Simetri Lipat Jajar Genjang

Memahami konsep simetri lipat pada jajar genjang bisa menjadi lebih mudah dengan beberapa pendekatan berikut:

• Visualisasi: Gunakan model jajar genjang yang dapat dilipat. Coba lipat sepanjang berbagai garis dan amati apakah kedua bagian saling menutupi dengan sempurna.
• Perbandingan: Bandingkan jajar genjang dengan bentuk-bentuk lain yang memiliki simetri lipat, seperti persegi panjang atau belah ketupat. Perhatikan perbedaan pada posisi dan jumlah garis simetri.
• Eksplorasi: Gambarlah beberapa jajar genjang dengan ukuran dan bentuk yang berbeda. Cobalah untuk menemukan garis simetri lipat. Ini akan membantu memperkuat pemahaman bahwa jajar genjang umum tidak memilikinya.
• Pemanfaatan Alat: Gunakan perangkat lunak geometri interaktif untuk memutar dan melipat jajar genjang secara virtual. Ini akan memberikan pengalaman visual yang lebih jelas.
• Fokus pada Sifat: Ingatlah bahwa simetri lipat berkaitan dengan kemampuan suatu bangun untuk dipetakan pada dirinya sendiri melalui lipatan. Jajar genjang umum tidak memenuhi kriteria ini karena sifat-sifat sudut dan sisinya.

Aplikasi Praktis Konsep Simetri Lipat dalam Berbagai Bidang

Konsep simetri lipat, meskipun terdengar seperti konsep matematika yang abstrak, memiliki penerapan yang sangat luas dan praktis dalam berbagai bidang kehidupan. Pemahaman tentang simetri lipat, khususnya pada bentuk-bentuk geometri seperti jajar genjang, membuka pintu bagi solusi kreatif dan efisien dalam desain, arsitektur, dan bahkan pemecahan masalah sehari-hari. Mari kita telaah bagaimana konsep ini berperan penting dalam menciptakan keindahan, keseimbangan, dan efisiensi dalam berbagai aspek kehidupan.

Penerapan Simetri Lipat dalam Desain Grafis

Desain grafis adalah salah satu bidang yang sangat bergantung pada prinsip simetri lipat. Penerapan konsep ini tidak hanya menghasilkan karya visual yang estetis, tetapi juga membantu menciptakan logo dan ilustrasi yang mudah diingat dan efektif dalam menyampaikan pesan. Simetri lipat pada jajar genjang, meskipun tidak memiliki simetri lipat sempurna seperti persegi panjang atau belah ketupat, tetap dapat dimanfaatkan untuk menghasilkan desain yang menarik.

Dalam pembuatan logo, penggunaan jajar genjang yang disimulasikan dengan simetri lipat, misalnya, dengan menggabungkan beberapa jajar genjang yang disusun sedemikian rupa sehingga menciptakan ilusi simetri, dapat menghasilkan logo yang unik dan menarik perhatian. Contohnya, logo perusahaan yang menggunakan bentuk jajar genjang yang diputar dan dicerminkan untuk menciptakan kesan dinamis dan modern. Bentuk-bentuk dasar jajar genjang yang digabungkan dengan elemen lain dapat menghasilkan logo yang terlihat seimbang dan harmonis.

Selain itu, penggunaan warna dan tekstur yang tepat dapat semakin memperkuat kesan simetri dan memperkaya visual logo.

Dalam ilustrasi, simetri lipat pada jajar genjang dapat digunakan untuk menciptakan komposisi yang seimbang dan menarik. Misalnya, dalam ilustrasi pemandangan, penggunaan jajar genjang sebagai elemen dasar untuk membentuk bangunan atau objek lainnya dapat memberikan kesan kedalaman dan perspektif. Dengan memanfaatkan prinsip simetri lipat, ilustrator dapat menciptakan visual yang menarik dan mudah dipahami oleh mata. Penggunaan teknik layering dan gradasi warna juga dapat memperkuat kesan simetri dan memberikan dimensi pada ilustrasi.

Pentingnya simetri lipat dalam desain grafis juga terletak pada kemampuannya untuk menciptakan konsistensi visual. Dengan menggunakan prinsip simetri lipat, desainer dapat memastikan bahwa elemen-elemen desain, seperti logo, ikon, dan ilustrasi, memiliki tampilan yang konsisten di berbagai media dan platform. Hal ini penting untuk membangun identitas merek yang kuat dan mudah dikenali oleh konsumen. Dengan demikian, pemahaman tentang simetri lipat pada jajar genjang menjadi keterampilan penting bagi seorang desainer grafis.

Simetri Lipat dalam Arsitektur

Arsitektur adalah bidang lain yang sangat mengandalkan prinsip simetri lipat. Penerapan simetri lipat dalam desain bangunan bertujuan untuk menciptakan keseimbangan visual, harmoni, dan estetika yang menyenangkan bagi mata. Meskipun jajar genjang tidak memiliki simetri lipat yang sempurna, prinsip-prinsip yang mendasarinya dapat diterapkan untuk mencapai tujuan tersebut.

Dalam arsitektur, simetri lipat dapat digunakan untuk menciptakan fasad bangunan yang seimbang dan proporsional. Misalnya, penggunaan jajar genjang sebagai elemen dasar dalam desain jendela atau pintu dapat memberikan kesan dinamis dan menarik. Pengulangan elemen-elemen jajar genjang pada fasad bangunan dapat menciptakan ritme visual yang menyenangkan. Selain itu, penggunaan simetri lipat dalam tata letak ruang dalam bangunan dapat menciptakan suasana yang teratur dan harmonis.

Misalnya, penempatan jendela dan pintu yang simetris terhadap sumbu tengah ruangan dapat menciptakan kesan keseimbangan dan keteraturan.

Contoh nyata penerapan simetri lipat dalam arsitektur dapat dilihat pada berbagai bangunan bersejarah dan modern. Misalnya, pada bangunan-bangunan klasik, seringkali terdapat penggunaan simetri lipat yang sangat jelas pada fasad bangunan, dengan penataan elemen-elemen seperti kolom, jendela, dan pintu yang simetris. Pada bangunan modern, penggunaan simetri lipat mungkin lebih subtil, namun tetap berperan penting dalam menciptakan keseimbangan visual dan estetika. Penerapan simetri lipat pada jajar genjang dalam arsitektur tidak hanya menciptakan keindahan visual, tetapi juga dapat memberikan manfaat praktis, seperti meningkatkan efisiensi ruang dan pencahayaan alami.

Contoh Kasus Nyata Pemecahan Masalah

Pemahaman tentang simetri lipat pada jajar genjang dapat menjadi kunci dalam memecahkan masalah praktis di berbagai bidang. Kemampuan untuk mengidentifikasi dan memanfaatkan prinsip simetri lipat dapat membantu dalam menemukan solusi yang efisien dan efektif.

Sebagai contoh, dalam bidang teknik, pemahaman tentang simetri lipat dapat digunakan dalam desain struktur bangunan atau jembatan. Dengan memanfaatkan prinsip simetri lipat, insinyur dapat memastikan bahwa struktur bangunan atau jembatan memiliki stabilitas dan kekuatan yang optimal. Misalnya, dalam desain jembatan gantung, penggunaan simetri lipat pada penataan kabel dan tiang penyangga dapat membantu mendistribusikan beban secara merata dan mencegah kerusakan struktural.

Dalam bidang manufaktur, pemahaman tentang simetri lipat dapat digunakan dalam desain produk yang simetris, seperti peralatan rumah tangga atau komponen mesin. Hal ini dapat mempermudah proses produksi dan memastikan kualitas produk yang konsisten.

Contoh lain, dalam bidang seni dan kerajinan, pemahaman tentang simetri lipat dapat digunakan dalam desain pola dan motif. Misalnya, dalam pembuatan batik atau tenun, penggunaan prinsip simetri lipat dapat menghasilkan pola yang indah dan harmonis. Dengan memanfaatkan prinsip simetri lipat, seniman dan pengrajin dapat menciptakan karya seni yang memiliki nilai estetika tinggi dan mudah diingat oleh masyarakat. Pemahaman tentang simetri lipat pada jajar genjang, meskipun tampak sederhana, dapat memberikan dampak yang signifikan dalam pemecahan masalah praktis di berbagai bidang.

Manfaat Pemahaman Konsep Simetri Lipat

Pemahaman konsep simetri lipat memiliki banyak manfaat dalam kehidupan sehari-hari. Berikut adalah beberapa manfaat utama:

• Meningkatkan Kemampuan Visual: Membantu dalam memahami dan mengapresiasi keindahan visual di sekitar kita, mulai dari desain grafis hingga arsitektur.
• Meningkatkan Kemampuan Analisis: Membantu dalam mengidentifikasi pola dan hubungan dalam berbagai situasi, yang berguna dalam pemecahan masalah.
• Meningkatkan Kreativitas: Membantu dalam mengembangkan ide-ide kreatif dan inovatif dalam desain dan seni.
• Meningkatkan Efisiensi: Membantu dalam merancang solusi yang efisien dan efektif dalam berbagai bidang, seperti teknik dan manufaktur.
• Meningkatkan Kemampuan Komunikasi: Membantu dalam menyampaikan ide dan konsep secara visual dengan lebih efektif.

Skenario Pembelajaran Interaktif

Berikut adalah contoh skenario pembelajaran interaktif yang melibatkan penggunaan jajar genjang dan simetri lipat:

Judul: “Membangun Kota Impian dengan Jajar Genjang”

1. Pengantar: Siswa diperkenalkan pada konsep jajar genjang dan simetri lipat melalui presentasi singkat dan contoh visual.
2. Tugas: Siswa dibagi menjadi kelompok dan ditugaskan untuk merancang sebuah kota impian menggunakan jajar genjang sebagai elemen dasar bangunan.
3. Proses:
   • Siswa menggambar sketsa kota mereka, menggunakan jajar genjang dengan berbagai ukuran dan orientasi untuk membentuk bangunan, jalan, dan ruang terbuka.
   • Siswa menggunakan prinsip simetri lipat untuk menciptakan keseimbangan visual dan keindahan dalam desain kota mereka.
   • Siswa dapat menggunakan perangkat lunak desain grafis sederhana atau alat gambar manual untuk membuat desain mereka.
4. Presentasi: Setiap kelompok mempresentasikan desain kota mereka, menjelaskan bagaimana mereka menggunakan jajar genjang dan prinsip simetri lipat dalam desain mereka.
5. Diskusi: Guru memfasilitasi diskusi tentang berbagai pendekatan desain, manfaat simetri lipat, dan aplikasi praktis konsep ini.
6. Evaluasi: Guru memberikan umpan balik konstruktif pada desain siswa dan menilai pemahaman mereka tentang konsep jajar genjang dan simetri lipat.

Tantangan dan Miskonsepsi Umum tentang Simetri Lipat pada Jajar Genjang

Simetri lipat pada jajar genjang, meski konsepnya sederhana, seringkali menjadi sumber kebingungan bagi banyak siswa. Memahami tantangan dan miskonsepsi yang umum terjadi adalah langkah krusial untuk menguasai konsep ini sepenuhnya. Mari kita bedah beberapa poin penting yang seringkali menjadi hambatan dalam perjalanan belajar.

Miskonsepsi Umum dan Solusi

Terdapat beberapa kesalahpahaman umum yang kerap muncul saat mempelajari simetri lipat pada jajar genjang. Mengidentifikasi dan mengatasinya adalah kunci untuk pemahaman yang lebih baik.

Salah satu miskonsepsi utama adalah anggapan bahwa jajar genjang memiliki simetri lipat seperti persegi panjang atau belah ketupat. Siswa seringkali salah mengira bahwa garis yang menghubungkan dua titik sudut yang berhadapan akan membagi jajar genjang menjadi dua bagian yang identik. Padahal, simetri lipat mengharuskan kedua sisi yang terlipat saling menutupi dengan sempurna.

Solusi untuk mengatasi hal ini adalah dengan menggunakan model konkret. Siswa dapat membuat jajar genjang dari kertas dan mencoba melipatnya. Dengan melakukan percobaan langsung, mereka akan menyadari bahwa tidak ada garis lipat yang dapat menghasilkan dua bagian yang saling menutupi dengan sempurna. Guru dapat memberikan contoh dengan persegi panjang dan belah ketupat sebagai pembanding, menunjukkan perbedaan jelas dalam kemampuan melipat.

Miskonsepsi lain muncul dari kurangnya pemahaman tentang definisi simetri lipat itu sendiri. Beberapa siswa mungkin berpikir bahwa asalkan bentuknya terlihat simetris secara visual, maka bentuk tersebut memiliki simetri lipat. Padahal, simetri lipat mensyaratkan bahwa ketika dilipat, kedua bagian harus sama persis dan saling menutupi.

Untuk mengatasinya, guru perlu menekankan definisi yang jelas tentang simetri lipat. Penggunaan animasi atau video yang menunjukkan proses pelipatan juga dapat membantu. Selain itu, siswa perlu diberikan latihan soal yang fokus pada identifikasi simetri lipat, dengan berbagai bentuk geometri sebagai variasi.

Terakhir, kesulitan sering muncul karena kurangnya visualisasi spasial. Siswa mungkin kesulitan membayangkan bagaimana sebuah bentuk akan terlihat setelah dilipat. Solusi untuk ini adalah dengan mendorong siswa untuk menggambar atau menggunakan software geometri interaktif. Dengan melakukan ini, siswa dapat memutar, membalik, dan melipat bentuk secara virtual, sehingga meningkatkan kemampuan visualisasi mereka.

Tantangan dalam Memahami Simetri Lipat pada Jajar Genjang dan Solusi

Memahami simetri lipat pada jajar genjang melibatkan beberapa tantangan yang perlu diatasi. Berikut adalah beberapa tantangan utama dan solusi yang bisa diterapkan.

• Kurangnya Pemahaman Konsep Dasar: Beberapa siswa mungkin belum memiliki pemahaman yang kuat tentang konsep dasar geometri, seperti garis, sudut, dan bentuk. Hal ini dapat menghambat kemampuan mereka untuk memahami simetri lipat.
• Solusi: Guru perlu memastikan bahwa siswa memiliki dasar geometri yang kuat sebelum membahas simetri lipat. Ini dapat dilakukan melalui pengulangan materi, penggunaan alat peraga, dan latihan soal yang relevan.
• Kesulitan Visualisasi Spasial: Siswa mungkin kesulitan membayangkan bagaimana bentuk akan terlihat setelah dilipat. Hal ini dapat menyulitkan mereka untuk mengidentifikasi garis simetri.
• Solusi: Gunakan model konkret, seperti kertas atau potongan karton, untuk membantu siswa memvisualisasikan proses pelipatan. Gunakan software geometri interaktif yang memungkinkan siswa untuk memutar dan membalik bentuk.
• Kesulitan Membedakan Simetri Lipat dengan Simetri Putar: Siswa mungkin bingung antara simetri lipat dan simetri putar.
• Solusi: Jelaskan perbedaan antara kedua jenis simetri ini secara jelas. Berikan contoh-contoh yang membedakan, dan berikan latihan soal yang fokus pada identifikasi kedua jenis simetri ini.
• Kurangnya Latihan: Siswa mungkin membutuhkan lebih banyak latihan untuk menguasai konsep simetri lipat.
• Solusi: Berikan siswa berbagai latihan soal yang melibatkan identifikasi garis simetri, menggambar garis simetri, dan menyelesaikan soal cerita yang berkaitan dengan simetri lipat.

Pertanyaan Umum tentang Simetri Lipat pada Jajar Genjang dan Jawabannya

Berikut adalah beberapa pertanyaan umum yang sering diajukan tentang simetri lipat pada jajar genjang, beserta jawabannya yang komprehensif.

• Apakah jajar genjang memiliki simetri lipat?

  Jawabannya adalah tidak. Jajar genjang tidak memiliki simetri lipat. Garis yang ditarik dari satu sudut ke sudut yang berlawanan tidak akan membagi jajar genjang menjadi dua bagian yang identik saat dilipat.

• Apa perbedaan antara simetri lipat dan simetri putar pada jajar genjang?

  Simetri lipat melibatkan kemampuan suatu bentuk untuk dilipat sehingga kedua bagian saling menutupi dengan sempurna. Jajar genjang tidak memiliki simetri lipat. Simetri putar, di sisi lain, melibatkan kemampuan suatu bentuk untuk diputar sehingga terlihat sama seperti bentuk aslinya. Jajar genjang memiliki simetri putar orde 2, yang berarti dapat diputar 180 derajat dan terlihat sama.

• Mengapa penting untuk memahami simetri lipat pada jajar genjang?

  Memahami simetri lipat membantu siswa mengembangkan pemahaman yang lebih baik tentang bentuk geometri dan sifat-sifatnya. Hal ini juga membantu mengembangkan kemampuan visualisasi spasial dan kemampuan memecahkan masalah.

• Bagaimana cara mengidentifikasi garis simetri pada suatu bentuk?

  Garis simetri adalah garis yang membagi suatu bentuk menjadi dua bagian yang identik. Untuk mengidentifikasi garis simetri, bayangkan atau lakukan pelipatan bentuk tersebut. Jika kedua bagian saling menutupi dengan sempurna, maka garis lipat tersebut adalah garis simetri.

Perbandingan Simetri Lipat dan Simetri Putar pada Jajar Genjang, Jajar genjang memiliki berapa simetri lipat

Perbedaan mendasar antara simetri lipat dan simetri putar pada jajar genjang perlu dipahami dengan jelas.

Simetri lipat, seperti yang telah dibahas, tidak dimiliki oleh jajar genjang. Jika kita mencoba melipat jajar genjang, tidak akan ada garis lipat yang menghasilkan dua bagian yang saling menutupi dengan sempurna. Hal ini berbeda dengan bentuk-bentuk seperti persegi panjang atau belah ketupat, yang memiliki simetri lipat.

Simetri putar, di sisi lain, dimiliki oleh jajar genjang. Sebuah jajar genjang memiliki simetri putar orde 2. Ini berarti bahwa jika jajar genjang diputar sebesar 180 derajat (setengah putaran penuh) di sekitar titik pusatnya, bentuknya akan terlihat sama seperti bentuk aslinya. Contohnya, bayangkan sebuah jajar genjang dengan titik sudut A, B, C, dan D. Setelah diputar 180 derajat, titik A akan berada di posisi C, dan titik B akan berada di posisi D, namun bentuk keseluruhan jajar genjang tetap sama.

Perbedaan utama terletak pada prosesnya: simetri lipat melibatkan pelipatan, sedangkan simetri putar melibatkan rotasi. Jajar genjang hanya memiliki simetri putar, sementara tidak memiliki simetri lipat.

Sumber Belajar Tambahan

Untuk memperdalam pemahaman tentang simetri lipat pada jajar genjang, berikut adalah beberapa sumber belajar tambahan yang dapat dimanfaatkan:

• Buku:

  Buku-buku pelajaran matematika sekolah dasar dan menengah seringkali memiliki bab khusus tentang geometri, termasuk simetri lipat dan putar. Carilah buku yang menyertakan contoh-contoh soal dan latihan yang relevan.

• Website:

  Terdapat banyak website pendidikan yang menyediakan materi tentang geometri, termasuk simetri. Beberapa website menawarkan animasi interaktif yang dapat membantu memvisualisasikan konsep simetri. Contohnya adalah Khan Academy, yang memiliki video dan latihan soal gratis.

• Video:

  YouTube adalah sumber daya yang sangat baik untuk menemukan video pembelajaran tentang simetri. Carilah video yang menjelaskan konsep simetri lipat dan putar secara visual. Pastikan untuk memilih video yang dibuat oleh sumber yang kredibel dan mudah dipahami.

Penutupan Akhir

Mempelajari simetri lipat pada jajar genjang bukan hanya tentang menghafal rumus atau menggambar bentuk. Ini adalah tentang melihat dunia dari sudut pandang yang berbeda, menghargai keseimbangan dan harmoni yang ada di sekeliling kita. Ingatlah, setiap garis simetri adalah cerminan dari keindahan yang tersembunyi. Teruslah eksplorasi, dan biarkan geometri menginspirasi.

Jadi, setelah menyelami dunia jajar genjang dan simetri lipat, mari kita bawa pengetahuan ini ke dalam kehidupan. Jadikan setiap langkah sebagai kesempatan untuk melihat keindahan dalam matematika, dan jangan pernah berhenti belajar.