Bilangan Cacah Adalah Fondasi Matematika dan Perannya dalam Kehidupan

Bilangan cacah adalah gerbang menuju dunia matematika yang menakjubkan. Bayangkan, tanpa mereka, bagaimana kita bisa menghitung hari, mengukur waktu, atau bahkan memahami konsep dasar seperti jumlah dan urutan? Mereka bukan hanya angka; mereka adalah fondasi dari segala sesuatu yang kita pahami tentang kuantitas.

Mari kita selami lebih dalam. Bilangan cacah, dimulai dari nol dan berlanjut tanpa akhir, membentuk struktur yang memungkinkan kita untuk membangun pemahaman tentang matematika yang lebih kompleks. Dari perhitungan sederhana hingga teori bilangan yang rumit, mereka selalu ada, mendukung setiap langkah perjalanan kita dalam menjelajahi dunia angka.

Mengungkap misteri bilangan cacah sebagai fondasi matematika yang tak tergantikan: Bilangan Cacah Adalah

Mari kita selami dunia bilangan cacah, pilar kokoh yang menopang bangunan matematika. Bilangan cacah, seringkali dianggap sederhana, sebenarnya menyimpan kekuatan luar biasa. Mereka adalah blok bangunan dasar yang memungkinkan kita memahami dan mengelola dunia di sekitar kita. Tanpa bilangan cacah, konsep matematika yang lebih kompleks akan runtuh. Mari kita bedah esensi mereka, melihat bagaimana mereka bekerja dalam kehidupan sehari-hari, dan bagaimana mereka membuka pintu menuju pemahaman matematika yang lebih dalam.

Mari kita mulai petualangan pengetahuan ini! Pernahkah terpikir apa bedanya saat air membeku dan menguap ? Itu adalah dua sisi mata uang yang berbeda, tapi sama-sama penting dalam kehidupan. Kemudian, kita akan menyelami nilai-nilai luhur yang ada dalam Pancasila sebagai pandangan hidup bangsa , yang tak ternilai harganya. Jangan lupa, Indonesia itu istimewa, dan salah satu alasannya adalah mengapa Indonesia disebut sebagai negara maritim.

Terakhir, mari bergerak! Pelajari teknik dasar gerakan chest pass untuk menguasai lapangan!

Bilangan cacah, atau yang dikenal sebagai bilangan bulat non-negatif, adalah sekumpulan angka yang dimulai dari nol (0) dan berlanjut tanpa akhir: 0, 1, 2, 3, dan seterusnya. Mereka berbeda dari jenis bilangan lain karena beberapa alasan krusial. Pertama, mereka adalah bilangan yang paling mudah dipahami dan diakses, bahkan oleh anak-anak kecil. Kedua, mereka merepresentasikan kuantitas diskrit – kita menghitung benda dalam satuan utuh, bukan pecahan.

Ketiga, mereka adalah dasar dari sistem bilangan desimal yang kita gunakan sehari-hari. Perbedaan mendasar terletak pada bagaimana bilangan cacah merepresentasikan kuantitas. Bilangan cacah hanya merepresentasikan jumlah utuh, sedangkan jenis bilangan lain mencakup pecahan, desimal, dan bahkan bilangan imajiner. Misalnya, bilangan bulat mencakup bilangan negatif, yang tidak termasuk dalam himpunan bilangan cacah. Bilangan rasional mencakup pecahan, yang juga bukan bagian dari bilangan cacah.

Bilangan irasional, seperti pi (π) atau akar kuadrat dari 2, bahkan lebih jauh lagi dari konsep bilangan cacah. Keistimewaan bilangan cacah terletak pada kesederhanaan dan keterkaitannya dengan realitas fisik. Mereka memungkinkan kita untuk menghitung objek, mengukur waktu, dan memahami konsep dasar seperti penambahan, pengurangan, perkalian, dan pembagian. Tanpa pemahaman yang kuat tentang bilangan cacah, kita akan kesulitan memahami konsep matematika yang lebih kompleks.

Esensi Bilangan Cacah: Fondasi Matematika

Esensi mendasar dari bilangan cacah adalah representasi kuantitas yang paling sederhana dan intuitif. Mereka berbeda dari jenis bilangan lain dalam beberapa aspek krusial, yang menjadikannya fondasi penting dalam matematika. Mari kita telaah lebih dalam.

Bilangan cacah adalah bilangan bulat non-negatif, dimulai dari nol (0) dan berlanjut tanpa batas: 0, 1, 2, 3, 4, dan seterusnya. Mereka berbeda secara fundamental dari jenis bilangan lain dalam beberapa hal. Pertama, mereka mewakili kuantitas diskrit, yang berarti kita menghitung dalam unit utuh, bukan pecahan. Kedua, mereka adalah dasar dari sistem bilangan desimal yang kita gunakan sehari-hari. Ketiga, mereka menyediakan landasan untuk operasi aritmatika dasar seperti penambahan, pengurangan, perkalian, dan pembagian.

Perbedaan utama antara bilangan cacah dan jenis bilangan lainnya terletak pada representasi kuantitas. Bilangan bulat, misalnya, mencakup bilangan negatif, yang tidak termasuk dalam himpunan bilangan cacah. Bilangan rasional mencakup pecahan, yang juga bukan bagian dari bilangan cacah. Bilangan irasional, seperti pi (π) atau akar kuadrat dari 2, bahkan lebih jauh lagi dari konsep bilangan cacah. Perbedaan ini penting karena menentukan jenis masalah matematika yang dapat diselesaikan dengan masing-masing jenis bilangan.

Bilangan cacah sangat cocok untuk menghitung objek, mengukur waktu, dan memahami konsep dasar aritmatika. Bilangan bulat memungkinkan kita untuk mewakili konsep seperti utang atau suhu di bawah nol. Bilangan rasional memungkinkan kita untuk bekerja dengan pecahan dan proporsi. Bilangan irasional memungkinkan kita untuk bekerja dengan konsep seperti luas lingkaran atau panjang diagonal persegi.

Mengapa bilangan cacah menjadi landasan penting dalam matematika? Karena mereka adalah konsep paling dasar yang kita gunakan untuk memahami kuantitas. Mereka adalah titik awal untuk memahami semua konsep matematika lainnya. Tanpa pemahaman yang kuat tentang bilangan cacah, akan sangat sulit untuk memahami konsep matematika yang lebih kompleks seperti aljabar, geometri, atau kalkulus. Bilangan cacah menyediakan kerangka kerja untuk memahami bagaimana angka bekerja, bagaimana mereka berinteraksi satu sama lain, dan bagaimana mereka dapat digunakan untuk memecahkan masalah.

Memahami bilangan cacah adalah langkah pertama yang penting dalam perjalanan menuju penguasaan matematika.

Bilangan Cacah dalam Kehidupan Sehari-hari

Bilangan cacah meresap dalam kehidupan sehari-hari, seringkali tanpa kita sadari. Memahami bagaimana mereka digunakan dalam berbagai konteks membantu membangun intuisi matematis yang kuat. Berikut adalah beberapa contoh konkret:

Menghitung Jumlah Benda: Ini adalah aplikasi paling dasar. Saat kita menghitung apel di keranjang, jumlah teman yang hadir, atau jumlah halaman yang dibaca, kita menggunakan bilangan cacah. Kemampuan ini memungkinkan kita untuk memahami kuantitas dan membuat perbandingan.
Mengukur Waktu: Jam, menit, dan detik adalah representasi bilangan cacah. Kita menggunakan bilangan cacah untuk menjadwalkan kegiatan, memahami durasi, dan merencanakan hari kita. Memahami konsep waktu berdasarkan bilangan cacah membantu kita dalam perencanaan dan manajemen waktu.
Menghitung Uang: Nilai uang, baik itu rupiah, dolar, atau mata uang lainnya, dinyatakan dalam bilangan cacah (dan desimal). Kita menggunakan bilangan cacah untuk mengelola keuangan, membuat anggaran, dan melakukan transaksi. Pemahaman tentang bilangan cacah sangat penting untuk literasi finansial.
Menghitung Skor: Dalam olahraga, ujian, atau permainan, skor dihitung menggunakan bilangan cacah. Hal ini memungkinkan kita untuk membandingkan kinerja, mengukur kemajuan, dan menentukan pemenang. Sistem skor berbasis bilangan cacah memberikan struktur dan kejelasan dalam evaluasi.
Nomor Telepon dan Alamat: Nomor telepon, alamat rumah, dan kode pos menggunakan bilangan cacah. Mereka digunakan untuk identifikasi dan komunikasi. Pemahaman tentang sistem penomoran berbasis bilangan cacah penting untuk navigasi dan konektivitas.

Pemahaman yang kuat tentang penggunaan bilangan cacah dalam konteks sehari-hari membantu membangun intuisi matematis. Ketika kita secara konsisten menggunakan bilangan cacah dalam situasi nyata, kita secara alami mengembangkan pemahaman yang lebih dalam tentang bagaimana angka bekerja. Hal ini memfasilitasi pembelajaran konsep matematika yang lebih kompleks di kemudian hari. Misalnya, pemahaman tentang penambahan dan pengurangan melalui pengalaman sehari-hari akan mempermudah pemahaman konsep aljabar.

Perbandingan Jenis Bilangan

Berikut adalah tabel yang membandingkan bilangan cacah dengan jenis bilangan lainnya:

Jenis Bilangan	Definisi	Contoh
Bilangan Cacah	Bilangan bulat non-negatif	0, 1, 2, 3, 4, …
Bilangan Bulat	Bilangan cacah, bilangan negatif, dan nol	… -3, -2, -1, 0, 1, 2, 3, …
Bilangan Rasional	Bilangan yang dapat dinyatakan sebagai pecahan p/q, di mana p dan q adalah bilangan bulat dan q ≠ 0	1/2, -3/4, 5, 0.75
Bilangan Irasional	Bilangan yang tidak dapat dinyatakan sebagai pecahan p/q, di mana p dan q adalah bilangan bulat	π (pi), √2, e

Tabel ini memberikan gambaran yang jelas tentang perbedaan antara berbagai jenis bilangan. Memahami perbedaan ini sangat penting untuk memahami konsep matematika yang lebih kompleks.

Peran Bilangan Cacah dalam Konsep Matematika Lanjut

Bilangan cacah memainkan peran penting dalam konsep-konsep matematika yang lebih kompleks seperti aljabar dan kalkulus. Pemahaman awal tentang bilangan cacah memfasilitasi pembelajaran lanjut dengan menyediakan fondasi yang kokoh. Mari kita eksplorasi bagaimana hal ini terjadi.

Dalam aljabar, bilangan cacah digunakan untuk merepresentasikan variabel dan konstanta. Misalnya, dalam persamaan sederhana seperti x + 2 = 5, x adalah variabel yang mewakili bilangan cacah. Memahami konsep bilangan cacah memungkinkan siswa untuk memahami konsep dasar aljabar seperti penyelesaian persamaan, manipulasi ekspresi aljabar, dan pemahaman tentang fungsi. Operasi aritmatika dasar (penambahan, pengurangan, perkalian, dan pembagian) yang dipelajari dengan bilangan cacah menjadi dasar untuk operasi aljabar.

Pemahaman yang kuat tentang bilangan cacah mempermudah transisi ke aljabar karena siswa sudah familiar dengan prinsip-prinsip dasar yang mendasari. Sebagai contoh, memahami bahwa 2 + 3 = 5 membantu siswa memahami bahwa a + b = c, di mana a, b, dan c adalah variabel yang mewakili bilangan cacah.

Dalam kalkulus, bilangan cacah digunakan dalam konsep limit, turunan, dan integral. Meskipun kalkulus melibatkan bilangan real, pemahaman tentang bilangan cacah membantu dalam memahami konsep dasar seperti urutan bilangan dan konsep limit. Misalnya, konsep limit dapat dijelaskan menggunakan urutan bilangan cacah yang mendekati suatu nilai. Memahami konsep bilangan cacah memungkinkan siswa untuk lebih mudah memahami konsep kalkulus yang lebih abstrak. Misalnya, memahami bahwa turunan adalah laju perubahan dapat dikaitkan dengan perubahan bilangan cacah dalam fungsi.

Selain itu, bilangan cacah berperan penting dalam konsep matematika lainnya seperti teori bilangan, kombinatorika, dan teori himpunan. Dalam teori bilangan, bilangan cacah digunakan untuk mempelajari sifat-sifat bilangan bulat, seperti bilangan prima, faktor, dan kelipatan. Dalam kombinatorika, bilangan cacah digunakan untuk menghitung kombinasi dan permutasi. Dalam teori himpunan, bilangan cacah digunakan untuk mengidentifikasi kardinalitas himpunan. Pemahaman yang kuat tentang bilangan cacah memberikan fondasi yang diperlukan untuk mempelajari konsep-konsep ini.

Sebagai contoh, pemahaman tentang konsep faktorial (n!) yang digunakan dalam kombinatorika didasarkan pada pemahaman tentang perkalian bilangan cacah.

Pemahaman awal tentang bilangan cacah juga memfasilitasi pembelajaran lanjut dengan membangun intuisi matematis. Ketika siswa memiliki pemahaman yang kuat tentang bilangan cacah, mereka lebih mampu memvisualisasikan konsep matematika yang lebih kompleks dan memecahkan masalah dengan lebih efektif. Ini karena mereka memiliki fondasi yang kokoh untuk membangun pengetahuan mereka. Misalnya, siswa yang memahami konsep penambahan dan pengurangan dengan bilangan cacah akan lebih mudah memahami konsep operasi aljabar.

Miskonsepsi Umum dan Cara Mengatasinya

Ada beberapa miskonsepsi umum tentang bilangan cacah yang seringkali menghambat pemahaman siswa. Mengidentifikasi miskonsepsi ini dan menggunakan pendekatan pengajaran yang efektif sangat penting untuk memastikan pemahaman yang benar. Mari kita bahas beberapa miskonsepsi umum dan cara mengatasinya.

Miskonsepsi 1: Nol Bukan Bilangan. Beberapa siswa mungkin percaya bahwa nol bukan bilangan. Ini mungkin karena nol seringkali tidak terlihat ketika menghitung objek.

Cara Mengatasi: Gunakan contoh konkret untuk menunjukkan bahwa nol adalah bilangan yang mewakili “tidak ada”. Misalnya, tunjukkan keranjang kosong (nol apel) atau minta siswa untuk membayangkan tidak ada teman yang datang ke pesta. Tekankan bahwa nol adalah bilangan yang sama pentingnya dengan bilangan lainnya.

Miskonsepsi 2: Bilangan Cacah Selalu Dimulai dari 1. Siswa mungkin salah mengartikan bahwa bilangan cacah dimulai dari 1 karena mereka sering menghitung objek mulai dari 1.

Cara Mengatasi: Tekankan bahwa bilangan cacah dimulai dari 0. Gunakan garis bilangan untuk memvisualisasikan urutan bilangan cacah, dimulai dari 0. Berikan contoh yang menunjukkan penggunaan nol dalam kehidupan sehari-hari, seperti suhu 0 derajat Celcius.

Miskonsepsi 3: Operasi Matematika Selalu Meningkatkan Nilai. Siswa mungkin percaya bahwa operasi matematika selalu meningkatkan nilai. Misalnya, mereka mungkin kesulitan memahami bahwa pengurangan dapat menghasilkan nilai yang lebih kecil.

Cara Mengatasi: Gunakan contoh konkret untuk menunjukkan bahwa pengurangan dapat menghasilkan nilai yang lebih kecil. Misalnya, gunakan apel untuk menunjukkan bahwa jika kita mengambil beberapa apel dari keranjang, jumlah apel akan berkurang. Gunakan garis bilangan untuk memvisualisasikan penambahan dan pengurangan, menunjukkan bahwa pengurangan bergerak ke kiri (mengurangi nilai).

Miskonsepsi 4: Perbedaan Antara Bilangan Cacah dan Bilangan Bulat Tidak Jelas. Siswa mungkin bingung tentang perbedaan antara bilangan cacah dan bilangan bulat, terutama ketika diperkenalkan dengan bilangan negatif.

Cara Mengatasi: Buat perbandingan yang jelas antara bilangan cacah dan bilangan bulat. Gunakan garis bilangan untuk memvisualisasikan perbedaan, menunjukkan bahwa bilangan cacah hanya mencakup bilangan non-negatif, sementara bilangan bulat mencakup bilangan negatif. Berikan contoh konkret yang menunjukkan penggunaan bilangan bulat dalam kehidupan sehari-hari, seperti suhu di bawah nol atau utang.

Pendekatan pengajaran yang efektif untuk mengatasi miskonsepsi ini meliputi penggunaan visualisasi (seperti garis bilangan), contoh konkret, dan aktivitas praktis. Guru juga harus mendorong siswa untuk bertanya dan mengeksplorasi konsep secara mendalam. Menggunakan permainan dan teka-teki yang melibatkan bilangan cacah dapat membuat pembelajaran lebih menyenangkan dan membantu siswa mengembangkan pemahaman yang lebih kuat. Penting untuk secara konsisten mengoreksi miskonsepsi dan memberikan umpan balik yang positif untuk membangun kepercayaan diri siswa dalam matematika.

Dengan pendekatan yang tepat, siswa dapat mengatasi miskonsepsi dan mengembangkan pemahaman yang kuat tentang bilangan cacah.

Menjelajahi sejarah dan evolusi konsep bilangan cacah dari masa ke masa

Perjalanan bilangan cacah adalah kisah yang luar biasa, sebuah perjalanan panjang dari kebutuhan praktis manusia untuk menghitung hingga menjadi fondasi penting dalam matematika modern. Memahami sejarah dan evolusi bilangan cacah bukan hanya tentang mempelajari angka, tetapi juga tentang memahami bagaimana peradaban manusia berkembang, beradaptasi, dan berinovasi. Mari kita selami perjalanan menakjubkan ini, mengungkap bagaimana bilangan cacah telah membentuk dunia yang kita kenal.

Perkembangan Konsep Bilangan Cacah dari Primitif hingga Modern, Bilangan cacah adalah

Konsep bilangan cacah, yang tampak sederhana bagi kita sekarang, mengalami evolusi yang luar biasa panjang. Dimulai dari kebutuhan dasar untuk menghitung dan mencatat, konsep ini berkembang menjadi sistem yang kompleks dan canggih yang kita gunakan hari ini. Perkembangan ini didorong oleh kebutuhan praktis, penemuan-penemuan penting, dan kontribusi dari berbagai tokoh kunci sepanjang sejarah.

Pada awalnya, manusia primitif menggunakan metode yang sangat sederhana untuk menghitung, seperti menggunakan jari, batu, atau goresan pada tulang atau dinding gua. Sistem ini bersifat ad-hoc dan terbatas, tetapi cukup untuk memenuhi kebutuhan dasar mereka. Seiring waktu, kebutuhan akan perhitungan yang lebih kompleks muncul seiring dengan perkembangan peradaban. Lahirlah sistem bilangan yang lebih terstruktur.

Salah satu tonggak penting dalam perkembangan ini adalah munculnya sistem bilangan berbasis posisi, di mana nilai suatu angka bergantung pada posisinya dalam urutan. Sistem ini memungkinkan representasi angka yang lebih efisien dan memungkinkan perhitungan yang lebih kompleks. Bangsa Babilonia adalah salah satu peradaban pertama yang menggunakan sistem bilangan berbasis posisi, meskipun sistem mereka berbasis 60 (sexagesimal) daripada 10 (desimal) yang kita gunakan sekarang.

Tokoh-tokoh kunci yang berkontribusi pada perkembangan bilangan cacah sangat banyak. Matematikawan India, seperti Aryabhata dan Brahmagupta, memainkan peran penting dalam pengembangan sistem bilangan desimal dan konsep nol. Penemuan nol, yang awalnya dianggap sebagai konsep yang sulit dipahami, adalah terobosan besar yang memungkinkan perkembangan matematika yang lebih lanjut. Nol memungkinkan kita untuk mewakili konsep “tidak ada” dan juga memfasilitasi perhitungan yang lebih efisien.

Perkembangan sistem bilangan desimal kemudian disebarluaskan ke dunia Barat melalui karya matematikawan Arab, seperti Al-Khwarizmi, yang memperkenalkan angka-angka India ke Eropa. Karya Al-Khwarizmi, khususnya bukunya “Kitab al-Jabr wa al-Muqabala,” memperkenalkan aljabar dan metode perhitungan baru yang sangat memengaruhi perkembangan matematika di Eropa.

Dari sistem perhitungan primitif hingga notasi modern, perjalanan bilangan cacah mencerminkan perkembangan peradaban manusia. Setiap langkah, dari penemuan sederhana hingga konsep yang kompleks, membuka jalan bagi kemajuan ilmu pengetahuan dan teknologi yang kita nikmati hari ini.

Timeline Tonggak Sejarah Penting dalam Pengembangan Bilangan Cacah

Berikut adalah timeline yang merangkum tonggak sejarah penting dalam pengembangan bilangan cacah:

Zaman Prasejarah: Manusia menggunakan jari, batu, dan goresan untuk menghitung.
3400 SM: Bangsa Sumeria mengembangkan sistem bilangan berbasis sexagesimal (basis 60).
3000 SM: Bangsa Mesir menggunakan sistem bilangan hieroglif.
1800 SM: Bangsa Babilonia mengembangkan sistem bilangan berbasis posisi.
300 SM: Bangsa Yunani mengembangkan sistem bilangan alfabetis.
Abad ke-3 M: Matematikawan India mengembangkan sistem bilangan desimal berbasis posisi, termasuk konsep nol.
Abad ke-9 M: Matematikawan Arab memperkenalkan angka-angka India ke Eropa.
Abad ke-12 M: Penerjemahan karya Al-Khwarizmi ke dalam bahasa Latin menyebarkan sistem bilangan desimal ke Eropa.
Abad ke-16 M: Sistem bilangan desimal mulai diadopsi secara luas di Eropa.
Abad ke-17 M: Isaac Newton dan Gottfried Wilhelm Leibniz mengembangkan kalkulus, yang sangat bergantung pada konsep bilangan cacah dan sistem bilangan.

Timeline ini menyoroti bagaimana penemuan nol dan sistem bilangan berbasis posisi merevolusi cara kita menghitung dan memproses informasi. Dampaknya terasa dalam setiap aspek kehidupan modern, dari teknologi informasi hingga ilmu pengetahuan.

Penggunaan dan Pengembangan Sistem Bilangan oleh Peradaban Kuno

Berbagai peradaban kuno mengembangkan sistem bilangan mereka sendiri, yang mencerminkan kebutuhan dan karakteristik budaya mereka. Sistem-sistem ini bervariasi dalam kompleksitas dan efisiensi, tetapi semuanya berfungsi untuk memfasilitasi perhitungan dan pencatatan.

Mesir Kuno: Bangsa Mesir menggunakan sistem bilangan hieroglif. Mereka menggunakan simbol-simbol yang berbeda untuk mewakili angka-angka seperti 1, 10, 100, 1000, dan seterusnya. Angka-angka ini ditulis dengan mengulang simbol yang sesuai. Meskipun sistem ini memungkinkan representasi angka yang besar, ia tidak efisien untuk perhitungan karena memerlukan banyak simbol. Sebagai contoh, angka 276 akan ditulis dengan dua simbol 100, tujuh simbol 10, dan enam simbol 1.

Babilonia: Bangsa Babilonia mengembangkan sistem bilangan berbasis posisi, yang merupakan terobosan besar. Sistem mereka berbasis 60 (sexagesimal), yang masih kita gunakan untuk mengukur waktu (60 detik dalam satu menit, 60 menit dalam satu jam). Mereka menggunakan dua simbol untuk mewakili angka: satu untuk satu dan satu lagi untuk sepuluh. Posisi simbol menentukan nilai angka tersebut. Sistem ini lebih efisien daripada sistem Mesir, tetapi tidak memiliki simbol untuk nol sampai lebih dari seribu tahun kemudian.

Romawi Kuno: Bangsa Romawi menggunakan sistem bilangan yang berbasis pada huruf-huruf alfabet. Mereka menggunakan simbol seperti I (1), V (5), X (10), L (50), C (100), D (500), dan M (1000). Angka-angka dibentuk dengan menggabungkan simbol-simbol ini. Misalnya, angka 1999 akan ditulis sebagai MCMXCIX (1000 + (1000 – 100) + (100 – 10) + (10 – 1)). Sistem Romawi relatif mudah dipahami, tetapi tidak efisien untuk perhitungan dan tidak memiliki konsep nol.

Perbandingan sistem-sistem ini menunjukkan perbedaan signifikan dalam pendekatan mereka. Sistem Mesir sederhana tetapi tidak efisien. Sistem Babilonia inovatif dengan basis posisinya, tetapi tidak memiliki simbol nol. Sistem Romawi mudah dipahami tetapi tidak praktis untuk perhitungan. Perbedaan ini mencerminkan kebutuhan dan prioritas yang berbeda dari masing-masing peradaban.

Perkembangan sistem bilangan ini menunjukkan kemampuan manusia untuk beradaptasi dan berinovasi. Setiap sistem memiliki kelebihan dan kekurangannya, tetapi semuanya berkontribusi pada perkembangan konsep bilangan cacah.

Pengaruh Bilangan Cacah pada Perkembangan Teknologi dan Ilmu Pengetahuan

Konsep bilangan cacah telah menjadi fondasi bagi kemajuan teknologi dan ilmu pengetahuan. Dari komputer hingga fisika kuantum, bilangan cacah adalah bahasa universal yang memungkinkan kita untuk memahami dan memanipulasi dunia di sekitar kita. Pengaruhnya sangat besar dan terus berkembang seiring dengan kemajuan teknologi.

Dalam bidang komputer, bilangan biner (basis 2), yang hanya menggunakan angka 0 dan 1, adalah dasar dari semua operasi. Setiap informasi, dari teks hingga gambar, direpresentasikan sebagai serangkaian angka biner. Prosesor komputer menggunakan gerbang logika yang beroperasi berdasarkan prinsip-prinsip bilangan biner untuk melakukan perhitungan dan memproses data. Tanpa bilangan cacah, komputer seperti yang kita kenal tidak akan ada.

Dalam bidang fisika kuantum, bilangan cacah digunakan untuk menggambarkan kuantisasi energi dan momentum. Partikel-partikel seperti elektron dan foton hanya dapat memiliki nilai energi tertentu, yang diwakili oleh bilangan cacah. Konsep ini sangat penting untuk memahami perilaku materi pada skala atomik dan subatomik. Contohnya, tingkat energi elektron dalam atom hidrogen dikuantisasi, yang berarti elektron hanya dapat berada pada tingkat energi tertentu, yang diwakili oleh bilangan cacah.

Dalam bidang matematika, bilangan cacah adalah dasar dari banyak konsep dan teori. Teori bilangan, misalnya, mempelajari sifat-sifat bilangan cacah. Konsep bilangan cacah juga penting dalam kalkulus, aljabar, dan geometri. Pengembangan teknologi dan ilmu pengetahuan modern sangat bergantung pada pemahaman dan penggunaan bilangan cacah.

Pengaruh bilangan cacah meluas ke berbagai bidang lain, termasuk keuangan, statistik, dan rekayasa. Dalam keuangan, bilangan cacah digunakan untuk menghitung bunga, investasi, dan transaksi keuangan lainnya. Dalam statistik, bilangan cacah digunakan untuk menganalisis data dan membuat prediksi. Dalam rekayasa, bilangan cacah digunakan untuk merancang dan membangun struktur, mesin, dan sistem lainnya.

Peran bilangan cacah dalam perkembangan teknologi dan ilmu pengetahuan sangat penting. Tanpa konsep bilangan cacah, kemajuan yang kita nikmati hari ini tidak akan mungkin terjadi. Bilangan cacah tetap menjadi alat yang tak ternilai harganya untuk memahami dan mengubah dunia.

Kutipan dari Ahli Matematika

“Bilangan cacah adalah dasar dari semua matematika. Tanpa mereka, kita tidak dapat membangun konsep yang lebih kompleks.”

David Hilbert, seorang matematikawan terkemuka.

Membedah sifat-sifat unik dan karakteristik esensial bilangan cacah

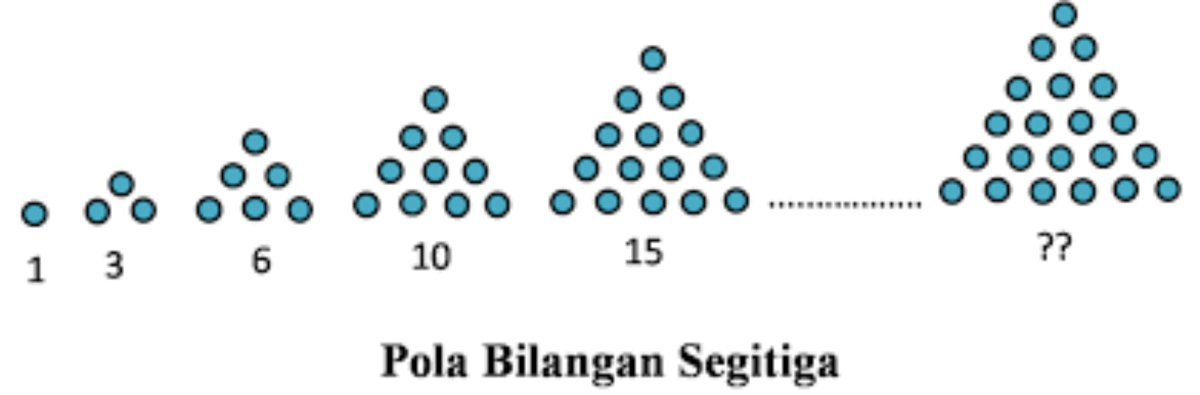
Source: co.id

Bilangan cacah, landasan dari matematika, lebih dari sekadar angka yang kita gunakan sehari-hari. Mereka memiliki sifat-sifat fundamental yang membentuk struktur matematika yang kita kenal. Memahami sifat-sifat ini membuka pintu ke dunia perhitungan yang lebih kompleks dan aplikasi yang tak terbatas. Mari kita selami dunia bilangan cacah, mengungkap keajaiban di balik angka-angka sederhana ini.

Sifat-sifat Dasar Bilangan Cacah

Bilangan cacah memiliki sifat-sifat dasar yang membangun fondasi matematika. Memahami sifat-sifat ini sangat penting untuk menguasai konsep matematika yang lebih lanjut. Mari kita telaah beberapa sifat kunci tersebut:

Urutan: Bilangan cacah memiliki urutan yang jelas, dimulai dari nol dan terus bertambah satu per satu (0, 1, 2, 3, …). Urutan ini memungkinkan kita membandingkan nilai bilangan cacah, menentukan mana yang lebih besar atau lebih kecil.
Kardinalitas: Kardinalitas mengacu pada jumlah elemen dalam suatu himpunan. Dalam konteks bilangan cacah, kardinalitas himpunan bilangan cacah tak hingga, yang berarti ada jumlah bilangan cacah yang tak terbatas.
Operasi Aritmatika: Operasi dasar aritmatika (penjumlahan, pengurangan, perkalian, dan pembagian) didefinisikan untuk bilangan cacah. Operasi-operasi ini memungkinkan kita untuk memanipulasi dan menggabungkan bilangan cacah untuk menyelesaikan masalah matematika.
Sifat Tertutup: Penjumlahan dan perkalian bilangan cacah selalu menghasilkan bilangan cacah. Ini berarti himpunan bilangan cacah bersifat tertutup terhadap operasi penjumlahan dan perkalian. Namun, pengurangan dan pembagian tidak selalu menghasilkan bilangan cacah (misalnya, 5 – 7 = -2, yang bukan bilangan cacah).
Identitas: Bilangan nol (0) adalah identitas penjumlahan, karena menambahkan 0 ke bilangan cacah tidak mengubah nilai bilangan tersebut (a + 0 = a). Bilangan satu (1) adalah identitas perkalian, karena mengalikan bilangan cacah dengan 1 tidak mengubah nilai bilangan tersebut (a
– 1 = a).
Sifat Komutatif, Asosiatif, dan Distributif: Sifat-sifat ini mengatur bagaimana operasi aritmatika dilakukan pada bilangan cacah, yang akan dibahas lebih lanjut.

Sifat-sifat ini, yang saling terkait, membentuk struktur matematika yang memungkinkan kita untuk membangun konsep-konsep yang lebih kompleks, mulai dari aljabar dasar hingga kalkulus. Pemahaman yang mendalam tentang sifat-sifat ini adalah kunci untuk menguasai matematika.

Penerapan Sifat Komutatif, Asosiatif, dan Distributif

Sifat komutatif, asosiatif, dan distributif adalah alat yang ampuh untuk menyederhanakan perhitungan dalam operasi bilangan cacah. Memahami dan menerapkan sifat-sifat ini dapat secara signifikan meningkatkan efisiensi dan keakuratan dalam memecahkan masalah matematika. Mari kita lihat bagaimana sifat-sifat ini bekerja:

Sifat Komutatif: Sifat komutatif menyatakan bahwa urutan operasi tidak memengaruhi hasilnya untuk penjumlahan dan perkalian.
- Contoh Penjumlahan: 3 + 5 = 5 + 3 = 8
- Contoh Perkalian: 2
  – 7 = 7
  – 2 = 14
Sifat komutatif memungkinkan kita untuk mengubah urutan angka dalam penjumlahan atau perkalian untuk mempermudah perhitungan.
Sifat Asosiatif: Sifat asosiatif menyatakan bahwa pengelompokan angka dalam penjumlahan atau perkalian tidak memengaruhi hasilnya.
- Contoh Penjumlahan: (2 + 3) + 4 = 2 + (3 + 4) = 9
- Contoh Perkalian: (2
  – 3)
  – 4 = 2
  – (3
  – 4) = 24
Sifat asosiatif memungkinkan kita untuk mengubah pengelompokan angka dalam penjumlahan atau perkalian untuk mempermudah perhitungan.
Sifat Distributif: Sifat distributif menghubungkan perkalian dengan penjumlahan. Ini menyatakan bahwa mengalikan suatu angka dengan jumlah dua angka lainnya sama dengan mengalikan angka tersebut dengan masing-masing angka dalam penjumlahan, lalu menjumlahkan hasilnya.
- Contoh: 2
  – (3 + 4) = (2
  – 3) + (2
  – 4) = 6 + 8 = 14
Sifat distributif sangat berguna dalam menyederhanakan ekspresi aljabar dan mempermudah perhitungan yang melibatkan perkalian dan penjumlahan.

Dengan memahami dan menerapkan sifat-sifat ini, kita dapat melakukan perhitungan dengan lebih efisien dan akurat, serta mengembangkan pemahaman yang lebih mendalam tentang struktur matematika.

Mari kita mulai dengan sesuatu yang sederhana, tapi penting: jelaskan perbedaan peristiwa membeku dan menguap. Memahami perubahan wujud ini adalah kunci untuk menguasai ilmu pengetahuan alam. Kemudian, kita beralih ke fondasi negara kita. Pancasila, sebagai pandangan hidup bangsa merupakan landasan yang tak tergantikan. Ingatlah selalu, ini adalah identitas kita! Kita juga punya kebanggaan sebagai negara maritim, dan ada alasan kuat mengapa mengapa indonesia disebut sebagai negara maritim.

Jangan lupakan semangat olahraga! Mari kita belajar tentang gerakan chest pass. Latihan terus, dan kamu akan semakin hebat!

Konsep Induksi Matematika

Induksi matematika adalah metode pembuktian yang kuat yang digunakan untuk membuktikan pernyataan yang berlaku untuk semua bilangan cacah. Metode ini didasarkan pada prinsip bahwa jika suatu pernyataan berlaku untuk kasus dasar (biasanya n = 1 atau n = 0) dan jika pernyataan tersebut berlaku untuk suatu bilangan cacah k, maka pernyataan tersebut juga berlaku untuk k+1, maka pernyataan tersebut berlaku untuk semua bilangan cacah.

Proses ini melibatkan dua langkah utama:

Langkah Dasar (Basis): Membuktikan bahwa pernyataan tersebut benar untuk kasus dasar (misalnya, n = 1).
Langkah Induksi:
- Hipotesis Induksi: Mengasumsikan bahwa pernyataan tersebut benar untuk suatu bilangan cacah k.
- Langkah Induktif: Membuktikan bahwa jika pernyataan tersebut benar untuk k, maka pernyataan tersebut juga benar untuk k+1.

Setelah kedua langkah ini selesai, kita dapat menyimpulkan bahwa pernyataan tersebut benar untuk semua bilangan cacah. Mari kita lihat contoh penggunaan induksi matematika:

Contoh: Membuktikan bahwa jumlah n bilangan cacah pertama adalah n(n+1)/2.
1. Langkah Dasar: Untuk n = 1, jumlah 1 bilangan cacah pertama adalah 1. Rumus memberikan 1(1+1)/2 = 1. Pernyataan benar untuk n = 1.
2. Langkah Induksi:
  - Hipotesis Induksi: Asumsikan bahwa jumlah k bilangan cacah pertama adalah k(k+1)/2.
  - Langkah Induktif: Kita perlu membuktikan bahwa jumlah k+1 bilangan cacah pertama adalah (k+1)(k+2)/2. Jumlah k+1 bilangan cacah pertama adalah jumlah k bilangan cacah pertama ditambah (k+1). Berdasarkan hipotesis induksi, ini sama dengan k(k+1)/2 + (k+1).
    Sederhanakan ekspresi ini: k(k+1)/2 + (k+1) = (k^2 + k + 2k + 2)/2 = (k^2 + 3k + 2)/2 = (k+1)(k+2)/2.
    
    Ini sesuai dengan yang ingin kita buktikan.
Karena langkah dasar dan langkah induksi berhasil, kita dapat menyimpulkan bahwa jumlah n bilangan cacah pertama adalah n(n+1)/2 untuk semua bilangan cacah n.

Induksi matematika adalah alat yang sangat berharga dalam matematika, memungkinkan kita untuk membuktikan pernyataan yang berlaku untuk sejumlah tak terbatas kasus. Ini sangat berguna dalam teori bilangan, aljabar, dan berbagai bidang matematika lainnya.

Bilangan Prima dan Komposit

Dalam dunia bilangan cacah, bilangan prima dan komposit memegang peranan penting. Mereka adalah blok bangunan dasar dari bilangan cacah lainnya, dan pemahaman tentang mereka sangat penting dalam teori bilangan. Mari kita bedah lebih dalam tentang apa itu bilangan prima dan komposit:

Bilangan Prima: Bilangan prima adalah bilangan cacah yang lebih besar dari 1 yang hanya memiliki dua faktor positif: 1 dan bilangan itu sendiri. Contoh bilangan prima adalah 2, 3, 5, 7, 11, 13, dan seterusnya. Bilangan prima tidak dapat dibagi secara merata oleh bilangan cacah lain selain 1 dan dirinya sendiri.
Bilangan Komposit: Bilangan komposit adalah bilangan cacah yang lebih besar dari 1 yang memiliki lebih dari dua faktor positif. Dengan kata lain, bilangan komposit dapat dibagi secara merata oleh bilangan cacah lain selain 1 dan dirinya sendiri. Contoh bilangan komposit adalah 4, 6, 8, 9, 10, 12, dan seterusnya.

Peran Penting dalam Teori Bilangan:

Faktorisasi Prima: Setiap bilangan komposit dapat difaktorkan menjadi perkalian bilangan prima. Ini adalah konsep dasar dalam teori bilangan dan memiliki banyak aplikasi, termasuk dalam kriptografi dan keamanan data. Contohnya, bilangan 12 dapat difaktorkan menjadi 2 x 2 x 3 (2 dan 3 adalah bilangan prima).
Saringan Eratosthenes: Algoritma klasik untuk menemukan semua bilangan prima hingga batas tertentu. Algoritma ini bekerja dengan mengeliminasi kelipatan dari setiap bilangan prima, meninggalkan hanya bilangan prima yang tersisa.
Distribusi Bilangan Prima: Memahami bagaimana bilangan prima didistribusikan di antara bilangan cacah adalah topik penelitian yang aktif dalam matematika. Teorema Bilangan Prima memberikan perkiraan tentang jumlah bilangan prima yang kurang dari atau sama dengan bilangan tertentu.

Bilangan prima dan komposit adalah elemen penting dalam matematika. Pemahaman tentang sifat-sifat mereka dan bagaimana mereka berinteraksi adalah kunci untuk memahami lebih dalam tentang struktur bilangan cacah dan aplikasinya di berbagai bidang.

Diagram Venn Himpunan Bilangan

Diagram Venn adalah alat visual yang sangat berguna untuk mengilustrasikan hubungan antara himpunan. Dalam konteks bilangan, kita dapat menggunakan diagram Venn untuk menunjukkan hubungan antara himpunan bilangan cacah, bilangan bulat, bilangan rasional, dan bilangan real. Berikut adalah penjelasannya:

Deskripsi Diagram Venn:

Bayangkan empat lingkaran yang saling tumpang tindih:

Lingkaran Terdalam: Bilangan Cacah (W): Himpunan bilangan cacah (0, 1, 2, 3, …) berada di dalam lingkaran terdalam.
Lingkaran Kedua: Bilangan Bulat (Z): Himpunan bilangan bulat (…, -3, -2, -1, 0, 1, 2, 3, …) berada di dalam lingkaran yang lebih besar, yang juga mencakup lingkaran bilangan cacah. Ini berarti semua bilangan cacah juga adalah bilangan bulat. Bilangan bulat mencakup bilangan cacah, serta bilangan negatif dari bilangan cacah.
Lingkaran Ketiga: Bilangan Rasional (Q): Himpunan bilangan rasional adalah lingkaran yang lebih besar lagi, mencakup lingkaran bilangan bulat. Bilangan rasional adalah bilangan yang dapat dinyatakan sebagai pecahan p/q, di mana p dan q adalah bilangan bulat, dan q tidak sama dengan nol. Ini mencakup semua bilangan bulat, pecahan, dan desimal berulang.
Lingkaran Terluar: Bilangan Real (R): Himpunan bilangan real adalah lingkaran terbesar, mencakup semua lingkaran lainnya. Bilangan real mencakup semua bilangan rasional, serta bilangan irasional (bilangan yang tidak dapat dinyatakan sebagai pecahan, seperti akar kuadrat dari 2 atau pi).

Penjelasan Singkat:

W ⊂ Z ⊂ Q ⊂ R: Notasi ini menunjukkan bahwa himpunan bilangan cacah (W) adalah subset dari himpunan bilangan bulat (Z), yang merupakan subset dari himpunan bilangan rasional (Q), yang merupakan subset dari himpunan bilangan real (R).
Hubungan Inklusi: Setiap himpunan termasuk dalam himpunan yang lebih besar. Misalnya, setiap bilangan cacah adalah bilangan bulat, setiap bilangan bulat adalah bilangan rasional, dan setiap bilangan rasional adalah bilangan real.
Visualisasi: Diagram Venn ini memberikan visualisasi yang jelas tentang bagaimana berbagai jenis bilangan berhubungan satu sama lain, yang membantu kita memahami struktur bilangan dalam matematika.

Diagram Venn ini membantu kita untuk memahami hierarki bilangan dan bagaimana berbagai jenis bilangan berhubungan satu sama lain, dari yang paling sederhana (bilangan cacah) hingga yang paling umum (bilangan real).

Aplikasi praktis bilangan cacah dalam berbagai bidang ilmu dan kehidupan

Bilangan cacah, seringkali dianggap sebagai konsep dasar matematika, ternyata memiliki peran yang sangat krusial dan serbaguna dalam berbagai aspek kehidupan. Dari dunia digital yang kompleks hingga keputusan finansial sehari-hari, bilangan cacah menjadi landasan bagi pemahaman, analisis, dan pengambilan keputusan yang efektif. Mari kita telusuri bagaimana bilangan cacah berkontribusi dalam berbagai bidang, memperlihatkan betapa pentingnya pemahaman terhadap konsep ini.

Penggunaan Bilangan Cacah dalam Ilmu Komputer

Dalam dunia ilmu komputer, bilangan cacah adalah fondasi dari segala sesuatu yang kita lihat dan lakukan. Mereka tidak hanya digunakan untuk menghitung, tetapi juga untuk merepresentasikan data, merancang algoritma, dan membangun struktur data yang kompleks. Tanpa bilangan cacah, komputer tidak akan mampu menjalankan tugas-tugas sederhana sekalipun.

Representasi data dalam komputer sebagian besar didasarkan pada sistem biner, yang menggunakan bilangan cacah 0 dan 1 untuk merepresentasikan informasi. Setiap karakter, angka, atau instruksi dalam program komputer pada akhirnya diterjemahkan menjadi urutan bilangan biner ini. Misalnya, huruf “A” dapat direpresentasikan sebagai 01000001 dalam kode ASCII. Ukuran file, jumlah piksel dalam gambar, atau kapasitas penyimpanan hard drive, semuanya diukur menggunakan bilangan cacah.

Algoritma, yang merupakan serangkaian instruksi yang dijalankan oleh komputer untuk menyelesaikan suatu masalah, juga sangat bergantung pada bilangan cacah. Algoritma pengurutan (seperti bubble sort atau quicksort) menggunakan bilangan cacah untuk membandingkan dan mengurutkan elemen dalam daftar. Algoritma pencarian (seperti binary search) menggunakan bilangan cacah untuk menemukan elemen tertentu dalam daftar yang sudah diurutkan secara efisien. Algoritma kompresi data menggunakan bilangan cacah untuk mengidentifikasi pola dan mengurangi ukuran file.

Struktur data, seperti array, linked list, dan tree, juga menggunakan bilangan cacah untuk mengelola dan menyimpan data. Array menggunakan indeks bilangan cacah untuk mengakses elemen-elemennya. Linked list menggunakan bilangan cacah untuk menyimpan alamat memori dari node-node berikutnya. Tree menggunakan bilangan cacah untuk merepresentasikan hubungan hierarkis antara data. Sebagai contoh, dalam sistem database, bilangan cacah digunakan untuk mengidentifikasi dan mengindeks catatan, memungkinkan pencarian dan pengambilan data yang cepat dan efisien.

Pemahaman tentang bagaimana bilangan cacah digunakan dalam struktur data memungkinkan programmer untuk merancang program yang lebih efisien dan efektif.

Contoh nyata penggunaan bilangan cacah dalam ilmu komputer mencakup:

Pemrosesan gambar: Setiap piksel dalam gambar direpresentasikan oleh bilangan cacah yang menunjukkan warna dan intensitasnya. Algoritma pemrosesan gambar menggunakan bilangan cacah untuk memanipulasi piksel, seperti mengubah kecerahan, kontras, atau menerapkan filter.
Pengembangan game: Posisi karakter, jumlah nyawa, skor, dan waktu dalam game semuanya direpresentasikan oleh bilangan cacah. Algoritma game menggunakan bilangan cacah untuk menghitung pergerakan, deteksi tabrakan, dan logika game lainnya.
Analisis data: Bilangan cacah digunakan untuk menghitung jumlah kejadian, frekuensi, dan statistik lainnya dalam analisis data. Algoritma pembelajaran mesin menggunakan bilangan cacah untuk mengolah data dan membuat prediksi.

Penggunaan Bilangan Cacah dalam Statistik dan Probabilitas

Statistik dan probabilitas memanfaatkan bilangan cacah sebagai alat utama untuk menganalisis data, menghitung peluang, dan mendukung pengambilan keputusan. Pemahaman yang kuat tentang bilangan cacah memungkinkan kita untuk menafsirkan informasi dengan lebih baik dan membuat kesimpulan yang lebih akurat berdasarkan data yang ada.

Dalam statistik deskriptif, bilangan cacah digunakan untuk menghitung ukuran pusat data, seperti rata-rata (mean), median, dan modus. Rata-rata adalah jumlah semua nilai dibagi dengan jumlah data, yang merupakan bilangan cacah. Median adalah nilai tengah dalam kumpulan data yang diurutkan, dan modus adalah nilai yang paling sering muncul. Ukuran penyebaran data, seperti rentang (range), varians, dan deviasi standar, juga dihitung menggunakan bilangan cacah.

Rentang adalah selisih antara nilai tertinggi dan terendah, varians mengukur seberapa jauh data tersebar dari rata-rata, dan deviasi standar adalah akar kuadrat dari varians.

Dalam probabilitas, bilangan cacah digunakan untuk menghitung peluang suatu kejadian. Peluang dihitung sebagai jumlah kasus yang menguntungkan dibagi dengan jumlah total kemungkinan kasus. Misalnya, peluang melempar dadu dan mendapatkan angka 4 adalah 1/6, karena ada satu kasus yang menguntungkan (mendapatkan angka 4) dan enam kemungkinan kasus (angka 1 hingga 6). Bilangan cacah juga digunakan dalam kombinatorika untuk menghitung jumlah cara berbeda untuk memilih atau mengatur objek.

Misalnya, berapa banyak cara berbeda untuk memilih 3 siswa dari 10 siswa? Rumus kombinasi menggunakan bilangan cacah untuk menghitung jumlah kemungkinan kombinasi.

Bilangan cacah memainkan peran penting dalam analisis data dan pengambilan keputusan. Misalnya, dalam penelitian pasar, bilangan cacah digunakan untuk menganalisis data survei, menghitung persentase responden yang memilih opsi tertentu, dan mengidentifikasi tren. Dalam bidang medis, bilangan cacah digunakan untuk menganalisis data klinis, menghitung tingkat keberhasilan pengobatan, dan membuat rekomendasi berdasarkan bukti. Dalam bisnis, bilangan cacah digunakan untuk menganalisis penjualan, mengidentifikasi peluang pasar, dan membuat keputusan investasi.

Melalui analisis data, kita dapat mengidentifikasi pola, membuat prediksi, dan mengoptimalkan strategi.

Contoh penggunaan bilangan cacah dalam statistik dan probabilitas meliputi:

Analisis survei: Menghitung persentase responden yang memilih opsi tertentu.
Perhitungan risiko: Menghitung peluang suatu kejadian yang tidak diinginkan terjadi, seperti kerugian finansial atau kecelakaan.
Pengujian hipotesis: Menggunakan bilangan cacah untuk menguji apakah ada perbedaan yang signifikan antara dua kelompok data.
Prediksi cuaca: Menggunakan model statistik yang melibatkan bilangan cacah untuk memprediksi cuaca di masa depan.

Penggunaan Bilangan Cacah dalam Ekonomi dan Keuangan

Dalam dunia ekonomi dan keuangan, bilangan cacah adalah alat yang tak tergantikan untuk memahami, menganalisis, dan mengelola sumber daya finansial. Mereka menjadi dasar untuk perhitungan, analisis, dan pengambilan keputusan yang memengaruhi setiap aspek ekonomi, mulai dari tingkat individu hingga skala global.

Perhitungan bunga adalah salah satu aplikasi paling mendasar dari bilangan cacah dalam keuangan. Bunga sederhana dihitung dengan mengalikan pokok pinjaman, suku bunga, dan jangka waktu pinjaman. Bunga majemuk dihitung dengan menambahkan bunga yang diperoleh ke pokok pinjaman, yang kemudian menghasilkan bunga lebih lanjut. Rumus bunga majemuk, misalnya, menggunakan bilangan cacah untuk menghitung jumlah uang yang akan diperoleh atau dibayarkan dalam jangka waktu tertentu.

Pemahaman tentang perhitungan bunga sangat penting bagi individu, perusahaan, dan pemerintah dalam mengelola keuangan mereka.

Inflasi, yang merupakan tingkat kenaikan harga barang dan jasa dalam suatu perekonomian, diukur menggunakan indeks harga konsumen (IHK) dan indeks harga produsen (IHP). Indeks-indeks ini menggunakan bilangan cacah untuk mengukur perubahan harga dari waktu ke waktu. Inflasi memengaruhi nilai uang, daya beli konsumen, dan keputusan investasi. Analisis inflasi membantu pembuat kebijakan dan pelaku ekonomi untuk memahami tren ekonomi dan membuat keputusan yang tepat.

Analisis investasi sangat bergantung pada bilangan cacah. Investor menggunakan bilangan cacah untuk menghitung tingkat pengembalian investasi (ROI), rasio harga terhadap pendapatan (P/E), dan metrik keuangan lainnya untuk mengevaluasi kinerja investasi. Mereka menggunakan bilangan cacah untuk membandingkan berbagai opsi investasi, menilai risiko, dan membuat keputusan yang tepat. Analisis investasi memungkinkan investor untuk memaksimalkan keuntungan dan meminimalkan risiko.

Keputusan finansial pribadi dan bisnis sangat dipengaruhi oleh bilangan cacah. Individu menggunakan bilangan cacah untuk mengelola anggaran, merencanakan pensiun, dan membuat keputusan pembelian. Perusahaan menggunakan bilangan cacah untuk mengelola arus kas, mengendalikan biaya, dan membuat keputusan investasi. Pemahaman tentang bilangan cacah memungkinkan individu dan perusahaan untuk membuat keputusan finansial yang lebih cerdas dan mencapai tujuan keuangan mereka.

Contoh penggunaan bilangan cacah dalam ekonomi dan keuangan meliputi:

Perencanaan anggaran: Menggunakan bilangan cacah untuk melacak pengeluaran dan pendapatan, serta membuat anggaran untuk masa depan.
Analisis pasar saham: Menggunakan bilangan cacah untuk menganalisis harga saham, volume perdagangan, dan metrik keuangan lainnya.
Perhitungan pajak: Menggunakan bilangan cacah untuk menghitung kewajiban pajak, seperti pajak penghasilan, pajak penjualan, dan pajak properti.
Analisis risiko kredit: Menggunakan bilangan cacah untuk menilai risiko kredit dan menentukan suku bunga pinjaman.

Penggunaan Bilangan Cacah dalam Bidang Teknik

Mari kita ambil contoh perhitungan struktural dalam teknik sipil. Dalam merancang jembatan, insinyur menggunakan bilangan cacah untuk menghitung beban yang akan ditanggung oleh struktur, seperti berat material, berat kendaraan, dan beban angin. Perhitungan ini sangat penting untuk memastikan bahwa jembatan tersebut aman dan mampu menahan beban yang diharapkan.

Langkah-langkahnya adalah sebagai berikut:

Pengumpulan Data: Insinyur mengumpulkan data tentang material yang digunakan, termasuk berat jenis, kekuatan tarik, dan modulus elastisitas. Data ini dinyatakan dalam bilangan cacah.
Perhitungan Beban: Insinyur menghitung beban mati (berat struktur itu sendiri) dan beban hidup (berat kendaraan dan orang yang melintas). Beban ini dihitung menggunakan bilangan cacah, seperti ton atau kilogram.
Analisis Struktur: Insinyur menggunakan perangkat lunak analisis struktur yang menggunakan bilangan cacah untuk mensimulasikan perilaku struktur di bawah beban. Perangkat lunak ini membagi struktur menjadi elemen-elemen kecil dan menghitung gaya dan tegangan pada setiap elemen.
Desain Elemen: Berdasarkan hasil analisis, insinyur merancang elemen-elemen struktural, seperti balok dan kolom, untuk memastikan bahwa mereka mampu menahan gaya dan tegangan yang terjadi. Dimensi elemen-elemen ini ditentukan menggunakan bilangan cacah, seperti panjang, lebar, dan tinggi.
Verifikasi: Insinyur memverifikasi desain dengan melakukan analisis tambahan dan memastikan bahwa struktur memenuhi semua persyaratan keamanan dan standar.

Contoh di atas menunjukkan bagaimana bilangan cacah digunakan secara sistematis dalam proses teknik untuk memastikan keamanan dan keberhasilan proyek. Analisis sistem lainnya, seperti analisis jaringan listrik atau analisis sistem kontrol, juga sangat bergantung pada penggunaan bilangan cacah untuk memodelkan, menganalisis, dan mengoptimalkan kinerja sistem.

Aplikasi Bilangan Cacah dalam Kehidupan Sehari-hari

Bilangan cacah adalah bagian tak terpisahkan dari kehidupan sehari-hari, mulai dari aktivitas sederhana hingga kegiatan yang lebih kompleks. Mereka membantu kita dalam mengukur, menghitung, dan memahami dunia di sekitar kita.

Berikut adalah beberapa contoh aplikasi bilangan cacah dalam kehidupan sehari-hari:

Memasak: Mengukur bahan-bahan dalam resep, seperti jumlah tepung, gula, atau telur yang dibutuhkan.
Belanja: Menghitung jumlah barang yang dibeli, total harga, dan uang kembalian.
Mengatur waktu: Menggunakan jam dan kalender untuk merencanakan kegiatan, mengatur jadwal, dan memperkirakan waktu yang dibutuhkan untuk menyelesaikan tugas.
Mengemudi: Memantau kecepatan kendaraan, jarak tempuh, dan jumlah bahan bakar yang tersisa.
Olahraga: Menghitung skor dalam pertandingan, jumlah repetisi dalam latihan, atau waktu tempuh dalam lomba lari.
Mengelola keuangan pribadi: Mencatat pengeluaran, menghitung saldo rekening bank, dan membuat anggaran.
Menggunakan teknologi: Menggunakan komputer, ponsel pintar, dan perangkat elektronik lainnya yang menggunakan bilangan cacah untuk berbagai fungsi, seperti menjelajah internet, mengirim pesan, atau bermain game.
Membaca berita: Memahami statistik dan data yang disajikan dalam berita, seperti jumlah kasus penyakit, tingkat pengangguran, atau pertumbuhan ekonomi.

Penutupan

Jadi, setelah menjelajahi berbagai aspek bilangan cacah, dari sejarah hingga aplikasinya, satu hal menjadi jelas: mereka lebih dari sekadar angka. Mereka adalah kunci untuk membuka pintu menuju pemahaman yang lebih dalam tentang dunia di sekitar kita. Memahami bilangan cacah bukan hanya tentang belajar matematika; ini tentang mengasah kemampuan berpikir logis, memecahkan masalah, dan melihat pola-pola yang tersembunyi dalam segala hal.

Jangan ragu untuk terus menggali dan menemukan keajaiban di balik angka-angka ini.